Building Calculus: A sample set of activities

In the last installment of this series on my Fall 2020 course preparations, I went into some depth on how learning activities would be handled. I presented some axioms for designing learning activities --- focus on active learning, begin and end with the learning objectives, and optimize F2F time for the middle third of Bloom's Taxonomy --- and outlined a modification of the seven-step lesson design framework that I use for flipped learning lessons that I wrote about at length in my book on flipped learning. But I stopped short of actually showing an example of learning activities that follow this process.
In this post, I want to rectify that situation and show the complete process for building learning activities for my fall Calculus class, including the activities themselves.
How class meetings work
First, I need to clarify the workflow of the class. Again, I'm focusing on Calculus right now because my other class (Discrete Structures) is going to work quite differently.
I wrote earlier about the "staggered hybrid" modality that I'm using, in which the students are split into two groups ("Team Red" and "Team Blue") with Team Red meeting F2F on Monday/Wednesday and Team Blue Tuesday/Thursday. This gives each team one day of F2F work on each part of a module; in lieu of a second day of F2F work on each part of a module, they will do asynchronous online activities that complete the lesson for that part of a module.
Here's a diagram that shows how it all fits together:
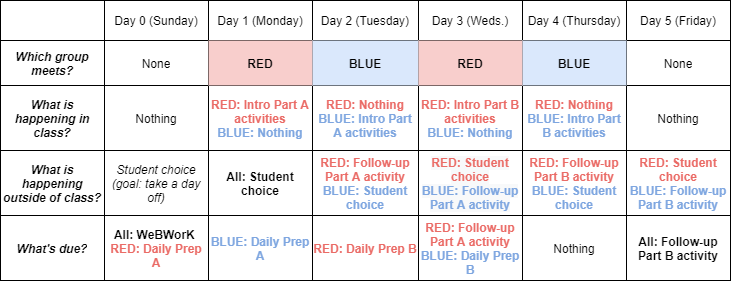
What this means for me, is that for each of the 12 modules of the course, I need to prepare two sets of learning activities (one set per part of a module). Each of those 24 sets has to consist of three things: A pre-class activity, in-class activities, and followup activities that complete the lesson and would be the equivalent of a second day of in-class activities. Additionally, as I'll describe in a future post, there are longer-term post-class activities in the form of learning target assessments and application projects, but these live outside the weekly workflow of the course.
Finally, an example
Let's look at a real example, starting --- appropriately --- with Module 1A from my Calculus course. This is the first lesson my students will encounter, and it focuses on how to find the instantaneous velocity of a moving object (Section 1.1 from Active Calculus).
In building the set of activities for this lesson, here's how each of the seven steps of my modified Bloom-centric process played out.
Step 1: Come up with learning objectives for the lesson
What I mean here isn't the module-level objectives I wrote about earlier because this lesson is only part of a module. Although, I'll note that this lesson does contribute to a module-level objective, namely:
L.1: (CORE) I can find the limit of a function at a point using numerical, graphical, and algebraic methods.
Limits do not actually make an appearance in Module 1A (they are the subject of Module 1B) but the concepts in 1A set the stage for the concept and provide a motivation for introducing it.
The learning objectives I need here are what I earlier called "micro-objectives" that are just things students need to learn how to do on the way to demonstrating mastery of the Learning Target above. Fortunately, I have already made a list of all the micro-objectives for the entire course, so all I have to do is cut and paste:
- Compute the average velocity of a function on an interval using either of the average velocity formulas.
- Explain the differences between average velocity and instantaneous velocity.
- Find the instantanous velocity of a moving object through a sequence of average velocities.
If you're playing along here with your courses, let me highly encourage you to invest time now and make a long list of all the micro-objectives for each section of your course. It will save a lot of time later.
Step 2: Remix the list in order of increasing complexity
Looking at the list of micro-objectives, I think it's already in the correct order. The first is simpler than the second, and the second simpler than the third. So there's nothing to do in this step. (This doesn't always happen; sometimes more difficult concepts appear before simpler ones.)
Step 3: Outline/rough out the in-class/F2F activity
Here's where the creative work begins. I have 50 minutes of F2F time with the students for this entire lesson that would ordinariy occupy two days of class. So I am going to focus on the middle 1/3 of Bloom's Taxonomy and those tasks that pertain not to basic knowledge but Applying and Analyzing that knowledge. This feels weird at first if you're not used to it because we tend to think first about what we students should do first. But here we are beginning with the middle in mind, and we will work backwards from here.
I'm just spitballing at this point, but an outline of what we can accomplish in F2F time is:
- An activity where students are given the position function of a moving object, then find average velocities around a particular time value (let's say $t=2$) on smaller and smaller time intervals, and then they're asked to estimate the instantaneous velocity. This is the heart of the lesson, the most important concept moving forward as well as the culmination of the first two micro-objectives.
- A peer instruction activity where students are given conceptual questions connecting average and instantaneous velocities to the slopes of secant and tangent lines. (This is not technically a micro-objective but it's an important concept that will come up later. Maybe I should add this to the micro-objective list for this lesson.)
- Those two activities should occupy the middle 30 minutes of the 50 minute session. The first 10 minutes can be a review of the pre-class activity (which we haven' written yet!) and time for Q+A, and the last 10 minutes can be there for slack time as well as for doing some kind of metacognitive wrap-up activity.
So, a decent outline. We'll come back to this in Step 5.
Step 4: Split the list of learning objectives
Having gotten my mind around what will take place in the F2F time, I can now see that students will be focusing on the third micro-objective; which means that they will need to learn the first two in their pre-class indepedent space. So the split of learning objectives into Basic and Advanced looks like this:
Basic learning objectives:
- Compute the average velocity of a function on an interval using either of the average velocity formulas.
- Explain the differences between average velocity and instantaneous velocity.
Advanced learning objectives:
- Find the instantanous velocity of a moving object through a sequence of average velocities.
Again, this split is important because it signals to students that they will not need to learn and understand everything about the lesson prior to class; just the first two items. And it creates a "to-don't" list for me, so that I don't spend time in class on basic stuff that is better spent on harder stuff.
Step 5: Write the in-class and followup activities
At this stage, I go back and revisit the outline and flesh it out into real activities. Here is the finished product:
A word about the packaging here: Given the pandemic, paper handouts are kind of a bad idea. I may also have students who cannot or choose not to attend the class in person. So the activities are always going to be in a digital format. Also, I'm using other digital tools here: Mentimeter for polling and peer instruction, Desmos for graphs, and the big central activity uses Google Spreadsheets. All of these are linked to the PDF of the slides, so the slides are like a home page for the activities. When we actually get to the first week of classes when this is deployed, I'll be creating a post on our class discussion board that has links to the slides and copies of all the links within the slides.
Update: In the comments, Felix asked to see what I was doing with Mentimeter. Here's an embed of the peer instruction questions. Hover your mouse at the very bottom of the image to see the toolbar that lets you advance; press "S" to hide the image and see the polling questions.
The "activities" are not all activities; there is some limited lecturing going on, and that's on purpose since this is the very first lesson in a freshman-level class --- having more guidance at the front end of a flipped or online class is probably a good thing while students are still getting oriented.
This set of activities gets us through what I would consider roughly the first half of the class treatment of the lesson. Ordinarily we would have a second day of work on this topic; but since this is a hybrid class, that day of work is converted to asynchronous online activities. That's what I'm calling "follow-up".
Here is the followup:
Students are supposed to complete these activities on their own time and submit them by the end of the day following their team's F2F meeting. I am deploying these using a tool called ClassKick. ClassKick lets me post activities and send them via a link to students; then students log in and can respond to the activities by typing directly onto them, or using a stylus, or working stuff out on paper and embedding a photo, or even leaving a voice response. The work shows up directly in ClassKick, so there's nothing for students to turn in --- they just do their work and it's done. If they need me to answer a question or check their work, there's a raise-hand feature; and when it's time to grade it, I just look through their work. The follow-up activities are graded with a check mark if it's complete and has a good faith effort.
Step 6: Write the pre-class activity
Now that the F2F and followup activities are done (although between now and September I will probably tweak things), it's time to write the pre-class activity that prepares students for them. This seven-step process saves the pre-class activity almost for last, because we start with the most valuable and limited resources we have --- the F2F meeting --- and figure out how to prioritize it, then work backwards.
Pre-class activities in Calculus are called "Daily Prep assignments". That's another name for the Guided Practice concept I've blogged about in the past and wrote about in my book. They consist of an overview of the lesson; the Learning Targets addressed and the split list of micro-objectives we did in Steps 1, 2, and 4; some video and text resources for learning; some exercises for practicing the basic objectives; and finally some instructions on doing and submitting the work.
Here is the final product:
The original on GitHub is here. Each of these will eventually be posted as Markdown, DOCX, and PDF files on the LMS, where students will access them. They are turned in the night before the lesson and are graded with a "check" if the work is complete (no blanks), has good faith effort (no responses of "I don't know"/"I don't understand"), and is turned in on time. This particular one is submitted via a Google Form, but others that I have coming up are in the form of a Desmos activity or something posted to ClassKick.
Step 7: Design longer-term post-class activities
There's not much to do in this step because the longer-term activities for this course come in the form of Learning Target assessments and application problems that are not part of the weekly workflow. I'll be saying more about this next time when I get into the assessment setup.
FAQs
Q: How much time does this take you?
A: Building all the items for this particular lesson took me about 3 hours --- but I spent a lot of time wrestling with new tools. In particular I created a LaTeX template for the F2F and followup activities, and it took me a solid hour just wrangling with LaTeX to get it to work. Now that it (seems to) work, though, it should save time overall. I estimate that eventually, 90 minutes should be sufficient on average to build one complete set of preclass, F2F, and follow-up activities.
Q: How many of these lessons do you plan to make before the class starts?
A: The goal is to have the first six weeks of the course completely built, loaded into the LMS, and ready to deploy on Day 1. That way, I can be on a schedule to complete one more week of lessons (roughly 3 hours of work by my estimates) during each week of the semester. I'll be happy if I can get the first 4 weeks done, and I'll accept just the first two weeks. Also, it's anybody's guess what the Fall semester will actually be like once it gets started, so I want to plan ahead but not too far.
Next time I'll talk about the assessments in the class, then about the grading setup. Meanwhile, ask me other questions in the comments.


