Building Calculus: A framework for learning activities

The building process for my Fall 2020 classes continues. I've been putting in roughly an hour a day for each course (Calculus, and Discrete Structures) with the eventual goal of having the main skeleton of the courses done by mid-July, and then focus on writing content for the courses through mid-August --- and having at least four weeks' worth of the materials for each course written, posted, and ready to roll by August 31. I'm setting that target for myself because I know Fall 2020 is going to be unlike anything I've experienced in 25 years of teaching, and I'm going to need the headspace to handle the corrections and adjustments I know I'll need to make, to say nothing of the emotional space I will need to attend to students, help colleagues, and take care of myself and my family. To "buy" that space and time later, I have to hit the ground running now.

In the last two posts on this subject, I wrote about how I decided on the "staggered hybrid" format for the course and on the foundation of the course, namely the learning objectives. This time I want get into the next step of the build, which as I wrote in my earlier series on how to get better at online teaching, is about the learning activities in the course.

Axioms for learning activities

As I wrote in that other post, a "learning activity" is something that a student does as some incremental step toward attaining a learning objective. These can take place anywhere and in any context --- online or F2F, in a synchronous meeting or asynchronously, done independently or in a group. If it's an activity that moves the needle on student mastery of a learning objective, it's a learning activity.

Ever since March, faculty have been asking --- with increasing frequency, and increasing intensity --- What are students supposed to do once we pivot to online instruction? This is a tough question, since Fall 2020's reality cuts against the basic assumptions of most of our instructional models. So we have to reset our thinking about how we make decisions about student learning activities. Others have written well about specific instructional methods that can pair productively with online or socially-distanced F2F teaching. Rather than reiterate this, I wanted to detail my general thinking process for selecting and designing activities for the Fall --- a framework that allows me to select from the many choices that are available and adapt them to what I want to accomplish with students.

First, I'm guided by three principles that I take as axioms of my instruction:

1. Active learning is central and indispensible. Whatever happens in my classes, whether it's in the F2F meetings or something done asynchronously, students need to be involved doing things and thinking about what they are doing. This is what makes active learning what it is. And I know enough about the effects of active learning --- that it improves student understanding of concepts, lowers failure rates, addresses core issues of equity in the STEM disciplines, and so on --- that the one thing I cannot ethically do is transition to passive pedagogies just because it would be easier.
2. Start and end with the learning objectives. A learning activity that's misaligned with learning objectives is just busy work. So the first step of selecting or building a learning activity must be What learning objectives are students working with? And the last step is Does that activity build skill with the learning objectives?
3. Optimize face-to-face time for the middle 1/3 of Bloom's Taxonomy. This needs a little more explanation. Back in this article about designing for flipped learning, I argued that Bloom's Taxonomy can be used to guide the design and management of flipped learning activities by focusing pre-class work on the lower 1/3 of Bloom, in-class activity on the middle 1/3, and post-class activity on the top 1/3:

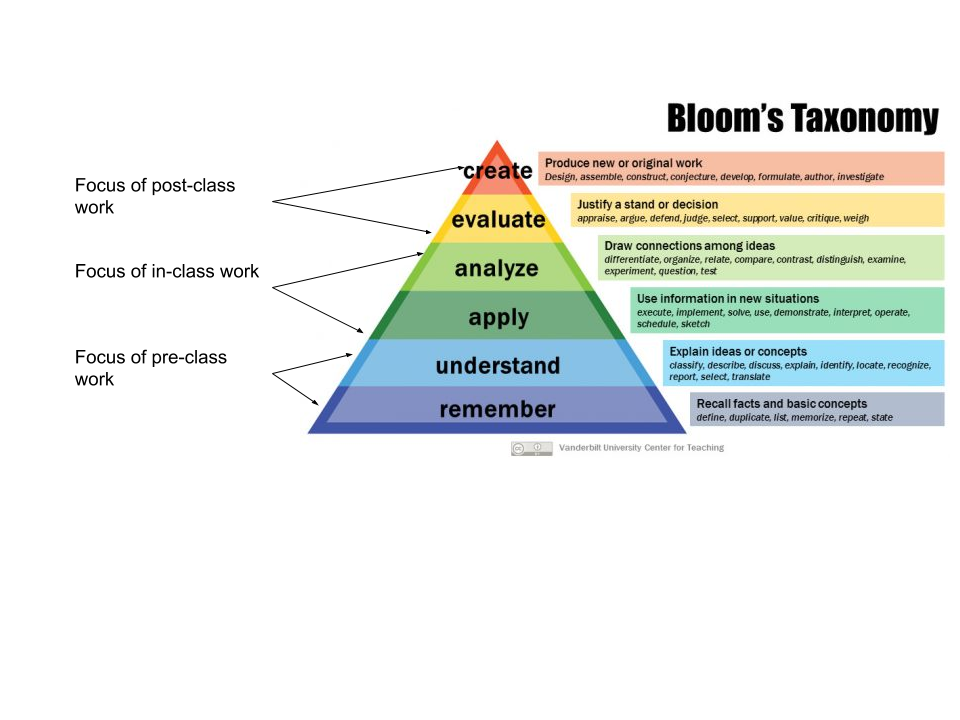
It strikes me that this is also a good design principle for online learning. My Fall classes do have F2F components at this point (assuming we aren't moving completely online before September), and we are carving out this F2F experience at great expense and considerable risk to those involved. It makes sense that we shouldn't waste it on activities at the bottom 1/3 of the cognitive ladder --- definitions of concepts, lists of facts, simple examples, etc. Those kinds of activities can, and should, be taken care of by students in their independent spaces. Instead, the really critical cognitive tasks --- the ones that act as culminations of all the basics, and gateways to all the more advanced work students should do --- are in the middle 1/3 of Bloom, in the form of Apply or Analyze tasks. And that's the proper focus of the F2F or synchronous time we are going to such lengths to secure for students.

Seven Steps revisited

To put this into practice, I'm going back to the seven-step flipped lesson design workflow that I wrote about in my book and in this free workbook. Briefly, that process for designing a single lesson for a flipped learning environment begins by listing the learning objectives for the lesson, remixing the list in order of complexity, then building the lesson --- first by focusing on the in-class (middle 1/3 of Bloom's Taxonomy) activities, then pre-class (bottom 1/3), then post-class (top 1/3). It's a process that's evolved over 10+ years of teaching with flipped learning that automates much of the thinking behind course prep and therefore saves me time, and keeps the lesson focused on the right things.

I'm modifying the process slightly for Fall because of the modalities of my courses. I'll focus on Calculus for the rest of this article. That course is set up to be like an ordinary course that meets MTWR for 50 minutes at a time --- except the F2F meetings are staggered, so half the class attends MW and the other half TR. The balance of the work is done asynchronously. Each topic takes roughly two days, so students will get F2F experiences for the first half of a topic and then will complete their work on it through asynchronous online work.

The main modification from a basic flipped learning environment is that whereas a basic environment involves a simple split between pre-class, in-class, and post-class activities that need to be designed, in my situation there are two kinds of "post-class" activities. There's the near-term post-class activity that's done asynchronously to replace one of the class meetings (and still addresses the middle 1/3 of Bloom), and there's the longer-term post-class activities like homework sets, projects, and so on that occupy the same space as regular post-class work in a flipped environment.

A smaller modification is that based on what I wrote last time, where the original process says "learning objectives", this means for me what I referred to as "micro-objectives" --- not the module-level objectives that I'll eventually assess but the fine-grained tasks that flow into those learning objectives.

So the modification of the seven-step process goes like this, with the changes in bold:

1. Come up with a brief but comprehensive list of learning objectives for your lesson.
2. Remix the learning objectives so that they appear in order of cognitive complexity.
3. Do a rough design of the in-class activity and the near-term post-class asynchronous activity you intend students to do.
4. Go back to the learning objectives list, and split it into Basic objectives and Advanced objectives.
5. Finish the design of the in-class activity and the near-term post-class asynchronous activity.
6. Design and construct the pre-class activity.
7. Design and construct any long-term post-class activities you intend students to do.

What's nice about this is that it's a familiar workflow since I've used it for flipped learning for a years, with only basic modifications. What's also nice is that I've already completed steps 1 for the entire semester, because I've already written out all the course- and module-level objectives as well as all the micro-objectives for the entire course and listed those by module. This is just one more instance of a central truth: Investing time to come up with clear and measurable learning objectives now, will save time later, like compounded interest.

Conclusion for now

I originally had a lengthy example of this process in action included as part of this article, but although it was lengthy, it wasn't complete in the sense that I didn't have actual handouts, slides, etc. to show how it all worked. So, rather than prolong this article, I'll follow up soon with a part 2 that shows how all this comes together and give you some actual honest-to-goodness-I'm-really-going-to-use-this materials to think about.

I'll just conclude by saying that choosing the instructional methods themselves --- group work or class discussions or think-pair-share or whatever --- is secondary. What's primary is having a consistent workflow for making these decisions, a framework that automates a lot of the thinking involved here and keeps me connected to my core pedagogical values and keeps students connected to the learning objectives. Fall 2020 is going to be chaotic enough! It's to our advantage to build systems now that will take the load off later.