Building Calculus: Assessments

Previously in this series on my Fall 2020 Calculus class, we've seen details on the choice of course modality, the construction of course- and module-level learning objectives, and the creation of synchronous and asynchronous learning activities that align with the learning objectives. This week, we take the next step and set up the system of assessments in the class.
What I mean by that term is the subset of activities that students will do in the class, that I formally evaluate for progress toward the learning objectives. Students will be doing a lot of activities but not all of these are graded; but many will be, and that collection and how they all work toward a common purpose in the course is what this post is about. This is not about the grading system in the course; that's coming up later and I have a lot to share about the mastery grading setup I'll be using. You'll get some taste of that system, however, in what I describe here.
A basis for assessment
There two essential properties that, in my view, an assessment system needs to have.
First, just like everything else, assessments should align with the learning objectives. There needs to be a clear line of sight between the assessments I give students and the course- and module-level learning objectives I've specified, otherwise it's likely that the assessment is not measuring what I want to measure, or measuring something that I've already measured sufficiently. Either way it's probably a waste of time for everyone. Having a clear path from assessments, backward to activities, backward to module-level objectives and finally back to the course-level objectives helps everyone realize that everything we do in the course is done with purpose.
Second, assessments should be minimal — as small of a number of them as possible, that will still produce reliable, actionable information about student learning. If I have two kinds of assessments that measure essentially the same thing, then unless one kind does it in a fundamentally different way than the other, I need to drop one from the syllabus. Or if a learning objective can be sufficiently observed through a combination of two assessments, I don't need a third to do the same thing.
In mathematics, we have a word for a set of objects that is minimal in size that gives complete information when those objects are used in combination with each other: It's called a basis.
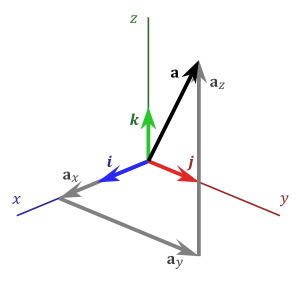
Sometimes the phrase minimal spanning set is used: Nothing unnecessary, no fluff and no fat on the one hand, and no learning objective left out on the other. The picture above shows how every point in 3D space can be reached simply by scaling and combining the three colored vectors. That's what I'm after in an assessment system: The ability to reach every point in the learning space of a student with just a small set of items.
In this post on mastery grading, I described a three-dimensional model that, in my view, builds a basis for assessment. In that model, assessments should occupy three separate dimensions: basic skill mastery, applications of basic skills, and engagement. I believe that the complete space of student learning in a course comes from a combination of these three things.
If you buy that, then the next question is: What is the smallest set of assessments I can give along each dimension that provides sufficient evidence in that dimension?
It's possible that one could design a course with just a single category of assessments in each dimension — for example, homework sets to assess basic skills, projects or programming assignments to assess application ability, and attendance to assess engagement. If that's the case, then that's the entire assessment system. We'd be tempted to add more assessments because it just feels like... not enough. But if I introduced quizzes, for example, then those might simply provide redundant information, telling me nothing I didn't already know through a combination of homework and projects. So I'd resist the temptation to add more to the system, and just keep it simple.
It's possible that a course could be designed with this super-minimal assessment scheme, but it seems hard to do so while making sure you're not losing critical information in the process. Does a combination of homework and projects really give me the same information as quizzes? Or might quizzes give me information about students' basic skill mastery, like homework, but in a fundamentally different way that would make quizzes worth the effort of adding?
So in building an assessment system, we have to strike a balance between simplicity on the one hand and completeness on the other. Too few assessments might fail to properly measure student learning in some important way. (This is the main problem with the old three-tests-and-a-final setup so many college classes still have.) Too many kinds of assessments, or too many of each kind, gives you lots of information but it's also lots of work for students and instructor alike (think about the grading involved), and we don't necessarily gain any new insights for all that work.
How it's working in Calculus
The Calculus course for Fall isn't completed yet, but the stable form of my assessments in that course is shaping up to be the following.
Basic skill mastery
Remember that the basic skills I want students to learn in the course are laid out in my list of Learning Targets (a.k.a. module-level objectives). There are 24 of these, 10 of which are designated as "Core" targets because they are the top-10 essential skills that students need to master in a Calculus course in my view. The other 14 are called "Supplemental" targets. These are assessed in two different ways.
First, online homework is assigned twice a week using the WeBWorK system. I will be assigning sets due Wednesday and Sunday each week, 8 problems each, each dealing with the learning targets for that part of the week plus regular review problems to promote interleaving and retrieval practice. Those problems are auto-graded by the system at 1 point each on the basis of whether the answer is correct or not.
Second, and less simple, student progress toward mastery of the Learning Targets is assessed through Checkpoints. Each checkpoint is a take-home exam consisting of one problem for each Learning Target that has been covered up to that point. For example the first Checkpoint might have problems for Learning Targets F.1, L.1, and D.1. The next Checkpoint might then have problems for Learning Targets D.2 through D.4, and new versions of the problems for F.1, L.1 and D.1. Then the third Checkpoint might have problems for Learning Targets D.5 through DC.2, and new versions of the problems for F.1 through D.4. And so on.
Each Checkpoint problem is graded with either a "check" or an "x" on the basis of whether the student's work on that problem meets the specifications or standards that I set for acceptable work on that problem. (Those specifications will be posted with examples at the beginning of the semester — that's a task I'm tackling next week.) So there are no points here, just a "good enough" or "not good enough". If a student's work isn't "good enough" (earns an "x") then the cumulative structure of those Checkpoints allows students to retake the problem in a new form at a later date. In fact on any given Checkpoint, a student only needs to work the problems that they feel ready to be assessed on. If they want to skip a Learning Target or two, they can do so and just circle back around to it later.
This is my online/hybrid answer to the concept in specifications grading of having reassessments. I don't want to rely on F2F meetings to do assessment or reassessment because students may not be able or willing to come to class at various points because of illness or wishing to avoid getting sick; and I think there's a very good chance we'll end up fully online at some point anyway. This cumulative structure is what George McNulty at the University of South Carolina used in his Calculus 2 course that's considered a prototype of specifications grading; I'm just stealing it and adapting it for online delivery.
But wait, there's more: Because I want to give students a lot of choice in how they are assessed, there are three other ways to earn a "check" on a Learning Target:
- Students can schedule an oral exam on a Learning Target over a videoconference.
- Students can create a video of themselves working out a Checkpoint-like problem at a whiteboard and send me the link.
- Students can use other forms of work, such as Application/Extension Problems (below) to argue that they have met the standard of a Learning Target.
The simple way to earn a check on a Learning Target is through a Checkpoint, and I expect the majority of students to use that method the majority of the time. But these other means work too, and having options is good.
I do place some restrictions on these alternative methods: Students can only opt to use one of these no more than once a week; and if they choose the second two, they have to schedule a followup meeting with me so I can probe them to make sure they really understand what they did.
Applications
Skill at applying the basics to new situations is assessed through one category of work: What I am calling Application/Extension Problems (AEPs). These will be similar to the "Challenge Problems" I described before and I have used these in past Calculus and Precalculus classes. They are, as the name suggests, problems where students have to apply or extend the basics in some way — usually involving data collection, modeling the data with an appropriate tool, and then performing some kind of calculus on it and interpreting the results. Here's an example of one from Precalculus to give the flavor.
AEP's are graded using the EMRN rubric:
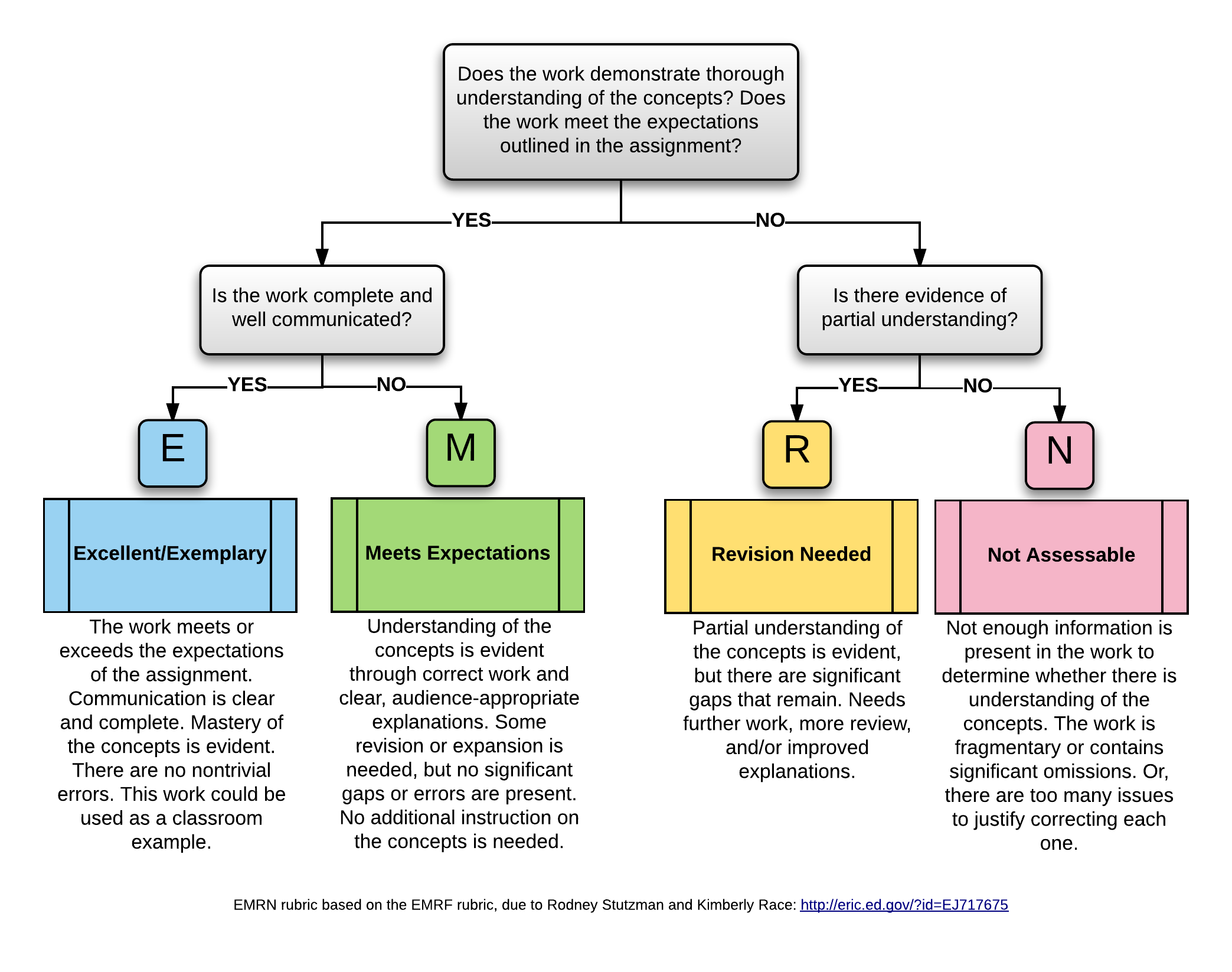
So again, no points, just a slightly more nuanced version of "good enough" or "not good enough". Work that is "not good enough" (R or N), or work that a student wants to push from Meets Expectations to Excellent, can be revised and resubmitted as often as the student wants. The only limitation is that only two AEP submissions can be made per week (2 new ones, 2 revisions, or 1 of each). Also, there are no deadlines on these except 11:59pm ET on December 11 — the last moment of the last day of classes. This is the quota/single deadline system that I described here.
Engagement
Engagement is a hard thing to define and therefore to assess. It wouldn't be wrong to question whether it belongs in an assessment system at all, since some would argue that a student's grade should be based solely on their mastery of the course content. But I've come to believe that engagement is very important, especially in online and hybrid courses, and it's worth it to have a simple system for assessing it that is lightweight and yet carries real consequences. So, for engagement, we have:
- Daily Preparation: This is what I am calling "Guided Practice" this semester to emphasize what it truly is — daily preparation for those F2F meetings that we are securing at such a great cost to ourselves. Aside from the name, it's the same as Guided Practice I've written about in the past (example, example): An overview of the part of the module for the day, learning objectives, resources for learning, and exercises. I posted the first one of these in an earlier article so you can see for yourself. Doing Daily Prep teaches you content, but more than that it keeps you engaged in the course. Daily Prep is graded check/x on the basis of completeness and effort only. (A "check" means the work was turned in on time, all the activities have something in them, and explanations show good-faith effort.)
- Followup Activities: Since we're hybrid this fall, the F2F meetings only go through about half of what a non-hybrid version of the course would. So the "day 2" of each module part is moved from an in-class activity to an asynchronous online activity, called Followup. I described these in the previous post in this series and mentioned that I am deploying them using a tool called Classkick. I've been increasingly impressed with Classkick the more I have been using it as I build both my courses out, and later on I hope to focus in on how it works. Followups are also graded check/x with the same criteria as Daily Prep.
- Engagement Credits: There are also going to be a lot of random things I want students to do during the semester that promote engagement. Those include informal mid-semester feedback surveys, filling out Five-Question Summary forms, completing an onboarding activity in week 1 where they learn the technology for the course, or even just giving credit for a particularly good discussion board contribution on the fly. So each student will have an account of engagement credits for doing those things. A student will earn those credits by doing things that keeps them plugged in and actively contributing to the learning community. Daily Prep and Followups will always be worth 1 engagement credit. Some will be more, like the onboarding activity. Then they just accumulate these credits through the semester. The way the schedule is shaping up, it looks like there should be at least 100 of those credits offered.
Conclusion
So that's the system:
- Checkpoints and WeBWorK for basic skills
- AEP's for applications
- Daily Prep, Followup, and random sources of engagement credits for engagement
There's one more thing: A final exam that will be given in the usual time that consists of a "big picture" section with items asking students to put some pieces together from throughout the course, and a final Checkpoint consisting of new versions of all 24 of the Learning Targets. I started introducing final exams to my specifications grading system a couple of years ago as a layer of information that promotes continued contact with early Learning Targets through the course. I don't particularly like giving a final, but this seems helpful and not too burdensome.
You are probably wondering how all of these things fit together. That's what I'll describe in the next post — how I bring all of these together under a mastery grading setup to determine students' course grades, and without using points!
Side note: There's a technical issue with the blog right now that is causing comments to close automatically after just 2-3 days. I'm trying to track the issue down. If you get locked out of the comments or replying to them, please send me your comment at robert.talbert@gmail.com and I will either reply personally or post all of them later.


