How do you measure active learning? And should you?

If you could measure how much active learning really takes place at your university, or any institution --- would you? How would you do it? And what would you do with the results?
These are questions I'm currently thinking about, in my new-ish role in our president's office. I'm sure they've been asked before; in fact I know they've been asked before on a smaller scale at my university. But as an institution-wide inquiry, this is new to me. And as is my practice, I'm using this blog to throw my dumb questions and imperfect thoughts on the matter out there to the internet in hopes of clarifying my thinking and getting some correctives.
What's this all about?
For about ten years, I've been working with faculty at institutions all over the US and in different countries to help them implement active learning in some way or another. Sometimes it's through a flipped learning workshop, or a talk about teaching with technology, and so on. In all this time and in all of these places, there's a core of faculty who are really committed to active learning and pushing it forward in their classes and throughout their institutions. But those institutions often don't share those commitments. Or, commitments to "student centered instruction", "lifelong learning", and so on — all of which have a practical embodiment in active learning — show up on paper, or on the strategic plan website, but you don't necessarily see those commitments play out in the average classroom.
In fact, I have recently been making this claim that if you picked a random college or university in this country, and then randomly picked 100 class meetings from that campus, you'd likely find 75 hour-long lectures and basically zero active learning. And that "75" figure would lock into place as you repeated the sampling process over and over across different classes and different schools.
This is a very quotable hot take that makes for good copy. But it's a quasi-statistical guess that I made up out of thin air, and I have no data to back it up. So, what if somebody did collect data on this? What if we had some way of knowing just how prevalent, or not, the use of active learning in actual classroom instruction is at an institution? That would be cool, either to either back this up or tell me that I'm wrong, or not grasping the nuances, or asking the wrong questions.
It also turns out that my boss wants to know.
I have a quarter-time appointment as "Presidential Fellow for the Advancement of Learning" through 2023. This involves working with our senior leadership team (the president, provost, and a few others) to coordinate large-scale initiatives for improving teaching and learning, for example running point on deploying active learning classrooms on two different campuses. I greatly enjoy this gig. This past year a major topic of conversation has been our new strategic plan that centers on three broad commitments: an empowered educational experience, educational equity, and lifelong learning. Like my hot take above, these are quotable and make for good copy. You can find some variation of these in just about any university mission statement. But if we're serious about these strategic commitments, I've wondered, then what are the tactical steps that we take to live them out? What do these look like in the day-to-day of the average student and faculty member?
It seems to me that the answer to that question is, they all look like active learning. All the available research points to the fact that active learning empowers students, erodes barriers to equity, and prepares students to be lifelong learners. Those of us who put active learning at the center of our teaching, don't need the research to tell us this. So in my view — and what I have said to my president — is that active learning is the tangible sign of being serious about actually making and sticking to those commitments. If we say we are committed to these three things, and yet our instruction is mostly passive, then something is out of kilter and perhaps we aren't as committed to our commitments as we think.
To which my president — being a clear thinker and someone who likes practical results — said: Sounds good, so where are we now on this? How much of our instruction right now is active learning? What sort of metric would you use to know, and to know if we're getting better? And so here we are.
What problem am I trying to solve?
The problem I am interested in solving is just a simple lack of knowledge about one question, which I currently am phrasing as: What proportion of the instructional time in our classes is spent on active learning? So the answer would be a number between 0 and 1 (or 0% and 100%) or perhaps an interval of numbers. That's it.
I know what you are probably thinking: This is stupidly reductive. The whole talk of "metrics" is gross and corporate. There are all kinds of dubious assumptions being made here. The number of confounding variables is off the charts. Investigating this sounds impossible, and to the extent it's possible it sounds expensive and horribly invasive. And so on.
I get it, and you're not wrong. But I'm also too curious to let the question go, just because there are some possible problems.
How would you even do this?
If you observed my Modern Algebra class and kept track of what went on, my guess is that you'd likely find that between 45 and 50 minutes of a 75 minute class is active learning in some form or another. That's roughly 60%-70% of the overall time in the meeting. So I want to point out that on an individual class scale, measuring the proportion of active learning used is completely doable. Unlike my hot take from earlier, that 60-70% figure is not made up. It's a guess, of course; but it's based on real experience, and it doesn't have to be a guess at all. Instead of guessing, I could ask a colleague who has a sound conception of what active learning is — someone who really knows the difference between "real" active learning and non-active learning — to come and do the observation, with some kind of a scorecard that records active learning episodes and how long they last. Then it's simple math: Add up the lengths of the episodes, and divide by 75.
So, if I were answering the main question just for myself, one way to do it is to have this longsuffering colleague observe all my classes (which is possible, thanks to Zoom recordings) and keep score on each one — tabulating the total active learning episode lengths of each session and finding the percentage, then just average the percentages over the whole semester. (I don't give timed tests, but if I had a "test day" then you could just not observe those since they're not regular class meetings.) This would give a percentage of active learning use for that course, in that semester, that is reasonably reliable.
That is to say, it's exactly as reliable as the observer, the instrument they are using to observe, and the validity of my operational definition of "active learning". All important notes that I'll come back to in a second.
Of course, any sane colleague would say "no" to a request to watch over 35 hours of class to record active learning episodes. Instead, I'd randomly select a subset of class meetings, have the colleague observe the sample, find the averages — and then use inferential statistics to make a claim about the percentage of active learning time for all my classes.
If you can imagine how this would work for one class section from one faculty member, it's an easy jump to see how it would work across a larger group: Just randomly select a bunch of class meetings across the university (throw out any exceptional ones — test days, lab sessions, small upper-level seminar courses. etc.). Then get a trained evaluator, or rather a team of trained evaluators; assign a chunk of the sampled class sessions to each one, and send them out to observe and score-keep on their assigned courses. Each session gets a percentage; then aggregate the percentages in a spreadsheet. The resulting Big Average Percentage is just for the sample, but again statistical techniques exist to make a claim about the "population" based on the sample.
So this is literally my hot take from earlier: Randomly select some classes, go see what's happening in those classes, and report back how often active learning takes place. Over repeated samples, the Central Limit Theorem states that your observed sample means will tend toward the population mean.
"But what about", part 1
I said earlier that this research would be exactly as reliable as the observer, the instrument they are using to observe, and the validity of my operational definition of "active learning". Let's get into each of those.
The instrument: It turns out there is more than one validated instrument for this very purpose. One of these is called the Teaching Practices Inventory and was developed by none other than Carl Wieman and Sara Gilbert; you probably know Wieman as a Nobel Prize-winning physicist who went on to turn his attention to problems in physics education and has pushed that part of STEM education a long way as a result. However, there are some issues with the TPI that make it not totally suitable for what I have in mind; I'll get into those in a later post.
Another instrument seems much more compelling – the Active Learning Inventory Tool (ALIT). It was developed by a team of pharmacy professors and validated by a number of recognizable experts in active learning. The latter includes Linda Nilson, and Charles Bonwell who is one-half of Bonwell and Eison who posited a definition of active learning that has become standard.
The ALIT does exactly what my thought experiment requires of an observational instrument. One one page, it lists 22 different active learning activity types, rank-ordered by "complexity" (the original term was "risk level") and given a shorthand code and a brief description:
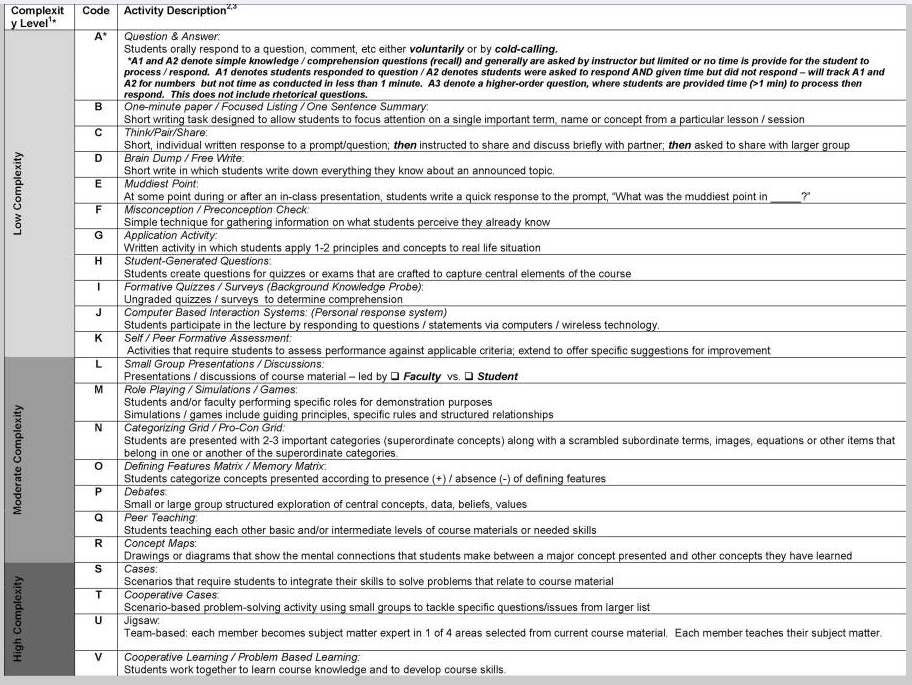
On the second page is room for recording demographic info and doing the scorekeeping:

What's nice about the ALIT is that it's fairly simple, it's undergone rigorous statistical validation, and it allows for later slicing of the data by a number of variables. For example, it would be interesting to correlate the amount of time spent on active learning with the "complexity" (again: risk) level of the activities; or the amount of high-complexity active learning with faculty rank and tenure status; and so on.
The operational definition: One of the great misconceptions about doing any sort of research on active learning is that there's no common definition. That's simply not true. Bonwell and Eison gave us one; and recently I wrote about an updated framework that in my view is even better. And another nice thing about the ALIT is that the 22-item list of activities is drawn from Bonwell and Eison (as the authors make clear in their paper) and essentially serves as the definition of active learning: Active learning is any activity that's a combination of these things. And in my view, it's hard to imagine an active learning task that can't be described in terms of the activities on their list.
The observers: So we totally have a usable definition here. The problem is inter-rater reliability — whether two different evaluators will interpret the same activity roughly the same way. That's a real issue, and the authors discuss it at some length in the paper. Basically, you can't just pull faculty members off the street to do this observation; there has to be training on how to recognize an activity, for example as "think/pair/share" and not the higher-complexity "small group presentations/discussions", although think/pair/share does involve discussing and presenting things in small groups. Unfortunately the authors don't include their training materials with the paper.
"But what about", part 2
Even if you accept that we have a usable definition of "active learning" for doing research with, and a good instrument, and at least an idea of how to train evaluators to use the instrument, there's still a lot of questions, perhaps the biggest of which is:
What's the population and how big of a sample do you need? I am (as should be obvious by now) not a statistician. But in my view, the "population" here would be the entire collection of individual class sessions taught at my university in a single semester, modulo any "non-standard" classes like small upper-level seminars, private music lessons, and the like. I did a back-of-the-napkin estimate on this: Our semesters are 14 weeks long and most faculty teach at least three classes, each of which often meets 3 times per week. (Sometimes it's 2, or 4; remember this is back-of-napkin stuff.) So a single faculty member will run about 126 class meetings in a semester. There are roughly 1700 teaching faculty of some form or another at my place. So that comes out to 214,200 class meetings overall. Let's round that to 200,000 to account for the non-standard classes, test days, and so on.
From that population, we will sample a sufficient number of class meetings, and have trained evaluators use the ALIT to measure the time spent on active learning in each meeting. What's "sufficient"? Well, according to this website – which uses statistical formulas that, again, I do not fully understand, so hold your fire here — in order have the Big Percent from the sample to have a 95% confidence level with a 5% margin of error, the sample size should be: 383 classes.
Now, that's a lot of observations for one person to do. But it's not that bad if you spread it out. What you could do, is recruit 40 people from among the faculty (and people from the Center for Teaching, with whom this whole thing should be coordinated); sample the class sessions and train the evaluators; then give each evaluator 10 meetings to observe. Set it up so it's no more than one class a week per evaluator — a roughly one hour weekly commitment. Then they go out and do their thing — collect data with the ALIT, feed it into a spreadsheet, and so on — once a week, until we're done. Just like that, we have 400 observations. (And pay those longsuffering evaluators somehow — reassigned time would be great, so would money or beer.)
I've run this by some statistics colleagues and asked them to poke holes in all this. I've been told that my population estimate is "really poor" (love the honesty) and I think they doubt my sanity even more than they used to, but otherwise the objections have been mostly aimed at the stuff in "Part 1" above.
But isn't this corporate, a violation of academic freedom, etc. etc.? I really don't think so. I don't think it's weird or creepy to want to know how often active learning really takes place versus how much we think it does or say that it does. I honestly would like to know, and if you really want to know, you have to collect some data. I don't believe those data should be used to evaluate people on any level. I don't have any preconception of what a "good" or "bad" percentage of active learning use should be — although I do personally think higher is better.
Would a study like this send a signal that we think active learning ought to be the default setting for faculty? Maybe — and honestly I am OK with that, given how much we know about how active learning helps students in precisely the ways that our strategic plan commits to.


