Using the computer as a tool for thinking in discrete mathematics

This article summarizes and extends a talk given at the AMS/MAA Joint Meetings on January 7, 2017. The website for the talk, with slides and links to resources, is at http://bit.ly/ctdiscrete.

Mathematics is a deep, broad, and beautiful subject that says profound things about our world. If that sentence causes cognitive dissonance with you, if it sounds like the complete opposite of your own concept of the subject, it's probably because the "mathematics" you learned in school isn't actually mathematics but some pale, impoverished cover version of mathematics. It might have looked instead like this:

• Memorizing facts without context
• Employing computational procedures without understanding the concepts
• Jumping from one fact or algorithm to another without grasping the connections
• Doing all this in an environment hermetically sealed from real life, or even just interesting questions

That's what it looked like for me, right up until the end of my secondary schooling. I could do the things my teachers were asking me to do; I had OK grades in math classes. I could even be motivated at times to get good grades in those classes. But my idea about the subject went no farther than the list above describes.

It wasn't until my senior year of high school in 1987, when I was taking AP Calculus, that a crack in that image formed, and I could see something a lot deeper through it.

How mathematicians are made

Two things happened. First, I had a teacher (Frances Allen) who had the gift so rare among teachers of knowing when to stop talking and let students try things on their own. Her classes were like workshops, where we kids had the time and space to try things, explore, make mistakes, and figure things out on our own terms. Second, during that year, I received what at the time was a revolutionary piece of technology:

This is the Hewlett Packard HP-28S graphing calculator. It has a tiny letterbox screen that was just big enough to graph $y = \sin(x)$. (And it uses reverse Polish notation which is also amazing, but that's another story.) It was easy to program, even for people like me who didn't really know how to program, and more importantly the graphing screen made it easy to screw around with ideas and see what transpired. For example, I'd graph $y = \sin(x)$. Then I'd wonder, What would happen if you graphed $y = \sin(2x)$ on top of it? Add in the new function, graph it side-by-side, and look at the results --- and then ask more questions. What about $\sin(3x)$? Or $\sin(4x)$? Or $\sin(-x)$? Pretty soon I'd have a theory of what's going on, and I could say something definitive about it and check my theory just as easily. And once I'd done all this, I wanted (even needed) to tell other people about it, and explain what I was seeing and why it worked.

I think I became a mathematician in Mrs. Allen's AP Calculus class. The confluence of being in an environment that stressed student exploration, and having the tools that made exploration systematic and easy, brought me to see that math is a lot more than algorithms and carrying out algorithms without screwing up. In fact screwing up honestly and scientifically is fundamental to the discipline. Mathematics, it turns out, is a way of creating new knowledge about the world and expressing that knowledge in a clear, logical, and ultimately true way. And I was hooked.

Computational thinking

I didn't know it then, but the process that I was discovering in Mrs. Allen's class with my HP-28S, that consists of coming up with a question to investigate and then:

1. Exploring that question by decomposing it into individual instances that can be run, checked and analyzed separately,
2. Then finding patterns among the individual instances,
3. Then forming an abstraction that attempts to give precise phrasing to the patterns I was seeing, and then finally
4. Designing an algorithm or explanation that explains why my abstraction was right,

-- this process had a name: computational thinking. The four parts of computational thinking are sometimes called decomposition, pattern finding, abstraction, and algorithm design.

The term "computational thinking" was popularized by Jeanette Wing in a paper in the Communications of the ACM in 2006 (PDF), and it's become popular as a concept in computer science education in the last ten years. But in fact, as Lorena Barba points out, the roots of computational thinking go back to Seymour Papert (of LOGO computer language fame), who was actually exploring this idea himself fairly close to the same time I was in Mrs. Allen's AP Calculus class.

Papert coined the term "computational thinking" in his landmark book Mindstorms: Children, Computers, and Powerful Ideas where he argued that school-aged children can, and should, learn mathematics by programming computers to do things. In his view, the computer was a "tool for thinking", a "Protean device" that can be made to perform whatever task the child wanted. But first, there must be the want; then the child programs the computer, rather than the computer programming the child. Papert foresaw the danger in the latter situation, and sadly this is how computer use in school mathematics has often played out: Children using computers to complete rote tasks that require conformity to the computer's way of doing things.

Computational thinking and discrete mathematics

Fast forward to the last three years. As a professor, I've been teaching a steady diet of discrete mathematics courses, particularly aimed at computer science majors. In these courses we study concepts that are foundational to the study of computing: logic, functions, sets, combinatorics, and mathematical proof in the first semester of the course and then recursion, graphs, relations, and trees in the second semester. While I think that Papert and Wing's idea of computational thinking works in almost all areas of mathematics, I think it has a special affinity for discrete mathematics because so much of discrete math is computational in nature. By this, I don't mean that most of what we do in discrete math is compute stuff. What I mean is that computation --- as an idea and a methodology --- is never far away from anything we do in this subject.

Take for example the classic beginning problem in set theory:

Given a finite set with $n$ elements, how many subsets does it have?

The answer is: $2^n$. We could simply tell students this fact and give them some reason to believe it. But it's a much more powerful thing to have students explore it on their own. And a computational thinking-oriented approach would look something like this:

1. Decomposition: Look at a few examples. What about the set ${a}$? Can we generate all its subsets? What about ${a, b}$? What about ${a,b,c}$? What about the empty set? (Answers are 2, 4, 8, and 1 respectively.) What about others? These are all easy questions to compute and check.
2. Pattern finding: Is there a pattern among the individual instances you computed? What if we made a table?
3. Abstraction: Can you put your observation into a concise, tight, clear, and correct mathematical statement? (Sure we can: For all nonnegative integers $n$, a set with $n$ elements has $2^n$ subsets. It might take an iteration or two to realize you have to quantify the variable properly.)

And then comes the hard part, algorithm or solution design. Consider one of the standard proofs of the conjecture:

(By mathematical induction) For the base case $n=0$, note that the empty set has 1 subset, namely the empty set. Now suppose that a set $S$ has $k$ elements for some positive integer $k$. Consider the $(k+1)$-element set $S' = S \cup {x}$ (where $x \not \in S$). The set $S$ has $2^k$ subsets by hypothesis. Those subsets are also subsets of $S'$. Additionally there are $2^k$ more subsets of $S'$ obtained by taking each of the subsets $S$ and unioning them with ${x}$. These are distinct from the subsets of $S$ because they all contain $x$. Therefore there are $2^k + 2^k = 2^{k+1}$ subsets of $S'$.

When you scratch the surface of this proof, what you see is that it's more than just an explanation for why the conjecture is true: It's actually a recursive algorithm for constructing the subsets themselves. The proof is not just explaining why there are $2^n$ subsets, but showing how to actually make those subsets.

That's why I say discrete mathematics is computational in nature. Not only is recursion in the DNA of the subject, even when recursion isn't clearly visible there is still a computational approach being taken in most cases.

Enter Python and Jupyter

My question for the last few years since I've been teaching discrete structures to CS majors has been, what are the best tools for using a computer as a tool for thinking, as Papert envisioned? I've bounced around with several platforms and I think I have found the one I like the most: A combination of the Python programming language and the Jupyter notebook platform. You probably have heard of Python. (If not, this sums it up.) But Jupyter might need some explanation.

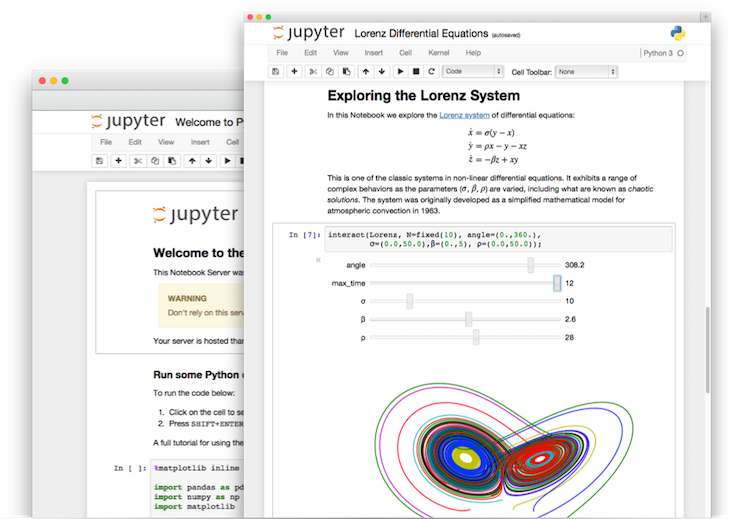
Jupyter (formerly known as iPython) is a free and open source platform that provides an interactive notebook-based user interface to existing computer languages. The image above shows Jupyter connecting to Python 3. You can also set up Jupyter to use SageMath, or R, or Haskell, or a number of other kernels.

What makes Jupyter special is that the interface allows users to combine executable code blocks and Markdown text and LaTeX, all in the same place --- and then share those notebooks with the world, either directly (for example by hosting them on GitHub or nbviewer) or by exporting to PDF or HTML or other formats.

This is a big deal for education. Using Jupyter, students and faculty have the means of creating professional, interactive computational documents that can themselves document the entire life span of a problem that students solve --- all the way from the decomposition phase where students are experimenting with examples, to writing up their thoughts on abstractions, to writing complete proofs of their conjectures. And don't forget that sometimes the answer to a mathematical question is not a proof but rather an actual algorithm, and if that's the case, then students can put the code right in the document along with any text they need. Jupyter notebooks are therefore like real, physical notebooks that scientists use that show the whole lifespan of a question being studied. And, again, it's free and open source, and accessible either as a local installation (using Anaconda) or in the cloud (using services like SageMath Cloud or Microsoft Azure).

One of my favorite examples of use with Jupyter notebooks and Python is this homework assignment, where students are tasked with writing a Python function rrsolver that will take in the coefficients on a second-order linear homogeneous recurrence relation along with two initial conditions, and then print off the closed-form solution. This requires serious computational thinking. Students have to solve specific examples of recurrence relations by hand first and pay attention to the process; figure out how the solution works out each time; phrase that pattern as a precise abstraction; and then write it into code. From my experience giving this assignment, you really don't understand how to solve a recurrence relation using characteristic roots until you work out this program!

I've also had students work with Python and Jupyter in class and through more extended mini-projects, sometimes where the solution to a problem is code and sometimes where coding is used to help motivate a proof. I have more example of use at http://bit.ly/ctdiscrete.

Final thoughts and FAQ's

I've come to believe that in a course like discrete mathematics, computational thinking is really the correct way to frame the design of the course and the learning goals for the students. If the students, like mine, also happen to be mostly computer science majors, then computational thinking is a natural bridge between the world of CS and math. (I've had students tell me that computational thinking is perfectly natural for them because this is the way they natively solve problems as programmers.) And it promotes the kind of lifelong learning skills that we ought to be teaching in our classes in any subject. And I really like the combination of Python and Jupyter as a way to get students using computer programming to learn those concepts.

Finally, some frequently asked questions about all this.

Q: Do your students know Python coming into the course?

A: Not uniformly. Some have used it before while some may be currently enrolled in their very first programming course. My usage of Python in the course assumes no prior knowledge of programming.

Q: Then how do they learn it? Do you spend class time teaching it?

A: For the last couple of semesters, I've had students go and work through the first 10 units of this free CodeAcademy Python course during the first three weeks of classes. I like this course because it's free, self-paced, covers all the basics (and nothing more), requires no installation of Python (it runs in the browser), and students can document that they've completed what they needed. It takes about 10---15 hours to complete on the average. I set a deadline of four weeks into the class to get it done, and then let students work at their own pace, then submit a screenshot of their completion (or show it to me in person) for credit. Before the deadline, I'm mainly using Python just as a demo. After that, we're using Python every day.

Q: Do students complain about this? Like, "This is a math class not a CS class"?

A: Sometimes. If I didn't use Python as a way of helping them learn mathematics, they'd have every right to do so. Therefore it's on me to make sure I'm not just tacking on a useless piece of cognitive load to the class but rather using the tool as a way to help them learn. To make this work, I have to constantly explain why we are doing what we're doing and stress the benefits. You want this to be germane load and not extraneous load.

Q: What about students who can't access the tools?

A: This is less of an issue than one might think. Python and Jupyter are available (freely) as downloads and installations for Windows, Mac, and Linux; and available in the cloud using SageMath Cloud or Azure. So the bottleneck is simply having a device to install it on, or access it in the cloud. A recent study found that 87% of college students own and use laptops, notebooks, or Chromebooks on a regular basis to do schoolwork^[1]. Chromebooks, in particular, are perfectly capable and relatively inexpensive ways to access these tools. My department recently bought five Chromebooks for $150 each, to give out as loaners to students who need them. Also consider that if you use a free and open source textbook for your class, it will save students as much as $150-250, which can then be reinvested in buying a computing device that will likely see a lot more use than a book.

Q: Why not use SageMath instead of Python? SageMath has tons of built-in features for discrete math, especialy graph theory.

A: It does indeed, and I used SageMath for a year in my classes. What I found was that it has a bit too much in the way of features. I want students in my classes to be developing a code base for working with discrete structures --- to build these by hand as much as possible, to really get into the details of how to make things work. SageMath, I found, had already built great code for everything I wanted students to do. Also, SageMath is not (as far as I know) available for local installation on Windows machines unless you're willing to install virtual machine software. A strong majority of my students are Windows users, and although they are CS majors, they are not always tech-savvy, and the workflow for getting SageMath to work locally on Windows was just more complex than I was comfortable asking them to deal with.

Q: Why not use CoCalc, if that's the case?

A: We did for a while, and CoCalc is an outstanding product, and running SageMath in a Jupyter notebook is just a matter of clicking a selection from a drop-down menu. However, students were using the free version that uses a public server, and they were constantly plagued by network timeouts and dropped connections. It was getting in the way of students doing work. I could either have had students pay for the upgraded version; or convinced my department to buy a departmental license; or just forget about SageMath and go back to straight Python where students had more options. I chose the latter. I'm happy with that choice because we are not bound to using something in the cloud.

Thanks for reading all this, and again for more information and resources visit the website for my talk at http://bit.ly/ctdiscrete.

Image credit: http://www.hpmuseum.org/hp28c.htm