Building Fall 2021: Discrete Structures

Fall semester for us starts exactly one month from today, so today I wanted to post a work-in-progress update on how I'm building my courses. I did this last year, although considerably earlier in the summer. I usually like to start building Fall courses in June, because I'm obsessive about taking my time with this. (Maybe just "obsessive".) I would have started earlier this year, but life intervened. My schedule was originally going to be three classes (two preps) — one section of our Functions and Models class and two of Discrete Structures for Computer Science 1. But due to some shuffling from enrollment changes and reassigned time (more on the latter, later) I'm left with just the Discrete Structures sections. I didn't want to start investing time and energy in prepping a course that might get canceled, so I waited until I was 90%-ish certain my schedule was a lock. That happened about a month ago, and I've been working on it ever since.

Here's where I am, for the benefit/commentary of everyone else in a similar situation. If you want to follow along or borrow from me, I keep all my materials on GitHub at https://github.com/RobertTalbert/discretecs.

Refresher on Discrete Structures

Discrete Structures 1 is the first of a two-semester course on discrete math aimed at computer science majors. It's required for our CS major as well as our new Cybersecurity major. The first semester focuses on foundations: integer representation in different bases, logic, sets, functions, combinatorics, and recursion/induction. The second semester focuses on proof techniques, relations, graphs and trees. Both courses are basically computer science courses taught out of the math department, and they're among my favorites for that reason. I really enjoy the students who gravitate to these courses, and I like how applicable the material is to real life while still being poised to consider deep mathematical ideas. I go out of my way to add these to my schedule when I can. I haven't taught the second semester in a while, but I taught the first course last Fall.

Modality and learning objectives

This time last year, I was (we all were) having serious discussions about the modality for Fall classes. This year, at least for now, there's no discussion: all our classes are face-to-face unless specifically advertised otherwise. How I feel about that is probably best discussed elsewhere, but in a nutshell, I'm slightly disappointed because I enjoy teaching online and would have been perfectly happy to do online courses this next year. The staggered hybrid model I used last fall wasn't a winner; students in the Discrete Structures course mostly opted out of the in-person meetings by mid-semester, making it a de facto online course, and it was fine — really good, actually. But that's theoretical for now. Except, I am keeping some options in reserve for switching the modality away from 100% in-person if, God forbid, the pandemic gets out of control.

So with the modality figured out, the next part of the course design is the most important: designing the learning objectives. These exist on two levels. The highest level, which we call the course-level learning objectives, are broad in scope and are mostly not "designed" by me but rather given in our department's syllabus of record which gives a core of high-level objectives that we have to include in syllabi, and we can add to those if we want. (Although I wrote the syllabus of record for this course, so there's not much to change and no room to complain.)

Although this isn't being taught as an online course, I find it helpful to adopt some practices from online teaching, especially breaking the course into modules. I created five modules for this course, one for each of the main ideas:

The main purpose of the modules is organization and labeling. Especially, the modules give me a skeleton framework for defining the second level of learning objectives, often called module level objectives which are more focused and actionable than the course level objectives. It's at the module level that we start to insist on using concrete action verbs and avoiding state-of-mind objectives like "know" and "understand". The module level objectives will also form the basis of the mastery grading system, below.

The module level objectives are called learning targets in my syllabus. There are 20 of these in all, 8 of which I have designated as Core targets. ($\LaTeX$ source here.)

This list required serious pruning and refactoring before I settled on 20 targets. I believe that when I first set down and brainstormed this list, it had 29 items on it. I prefer a rounder number for learning targets; so I edited and combined until I just so happened to have 20. I would have been OK with 25, but the editing process naturally led me to a smaller list.

Last year's class also had 20 learning targets but it's not the same 20 as this year's. For example, "I can compute a % b given integers a and b and perform arithmetic mod $n$" is gone, and is now part of the new objective SF.5 above. That's the result of experience — having a single objective for something so basic as computing a modulus was too fine-grained, and I found last fall that I wanted more evidence of students' ability to work with the special CS functions across the board. But the two lists are very similar otherwise.

Note that these module-level objectives are not the only things we study in the course — just the things I choose to assess in the course, which is a very different list. For example, we're learning Python on the course, but you don't see any Python learning objectives. I could have put some in that list and other profs might choose to do so. But for me, Python is a tool but not something I consider to be a core element of the course that makes a difference in students' course grades. Same for high-level learning objectives like you find in the course-level objectives list. These module-level objectives are much more "street level", the basic skills of discrete math that signal students' fluency with the central concepts.

Activities

With the learning objectives hammered out, we now ask What active learning tasks will students do to gain fluency with them? Well, it depends on the topic, but I'm keeping a running outline of what I think I'll do during class meetings to give students meaningful practice on these. I've got the first four weeks very generally mapped out so far, and the first week outlined in detail. Sometimes it's simple — for the class meeting about multiplication and division in binary (Learning Target CA.2) students will... work in groups to practice multiplying and dividing in binary. Although I'm throwing in some "what's the pattern?" questions too, for example What happens to the binary representation of an integer when you multiply it by 2? or 4? Or $2^n$? This is to get them used to explaining broader patterns.

But there are also activities before class since (as expected) I teach this class in a flipped learning structure. We don't have a textbook for the entirety of the class (although Levin's book does well for about half of it) so this summer I am making a playlist of videos to substitute for a written text:

This is a lot of work, but it's necessary given the state of not having a good textbook that fits how we teach the course. There will eventually be about 50 of these videos; six of them are on the playlist now and I made 3-4 more last year, so I should be able to get 1/3 of this done by August 30.

So in the flipped approach, students will watch these videos and do some reading, then complete some exercises on the lower-third-of-Bloom's-Taxonomy material prior to class meetings. Then the structure I have in mind for the meetings is:

• First 10 minutes: Students work in pairs to complete a worksheet based on the pre-class assignment, and we take time to field basic questions.
• Middle 30 minutes: Students work in groups of 3-4 on mid-level activities focused on applications.
• Final 10 minutes: We debrief the activity, take questions, and complete a brief metacognitive exit ticket.

Last year I attempted this structure and found that while students were completing the pre-class activities at a reasonable rate (usually at least 80% were doing the work), the depth of the work was just not sufficient to prepare them for the main activities. Students were doing the pre-class work but the understanding of that material was superficial. We would then end up spending not 10 minutes but 20-30 minutes fielding basic questions which left no time for the main activity. So I decided at the end of last semester that I simply need to get more out of my pre-class activities. That's the purpose for the pair-worksheet at the beginning of class.

Assessments

Now that we have learning objectives and activities to practice them, the question is What assessments will I give, to have students demonstrate their understanding? In recent years I have made this way too complicated with several threads of assessments that combine in complex ways, and it created a lot of work without a lot of return on investment. So this time I am going minimalist. There are only three main assessment types in the course:

• Daily Prep. This is the pre-class assignment plus the in-class pair worksheet I mentioned.
• Weekly Challenges. In previous iterations of the course I had "Challenge Problems" or "Application/Extension Problems" which were significant problems involving applications or extensions of the basic ideas and which required considerable time and effort for students. Nothing wrong with that; but these large-scale problems had no fixed deadlines, and I felt I was missing the weekly check-in from students that would give me an accurate read on their progress. Each Weekly Challenge will have ungraded practice problems (students can do them and turn in their work for feedback if they want to), some mid- to high-level application/extension problems, and a weekly check-in where they reply to prompts about how they are doing.
• Learning Target assessments. Students have the responsibility of demonstrating fluency on as many of the 20 Learning Targets as possible. They can do this in at least three ways. First, every couple of weeks we will have quizzes over the Learning Targets — each problem on a quiz covering just one target, and every quiz cumulative. Students can complete a quiz problem over a target. Or students can schedule an oral quiz with me, in office hours or on Zoom. Or students can make a video of themselves working out a quiz-like problem of my choosing and putting it on a private Flipgrid. Doing "satisfactory" work on any of these counts as a "successful demonstration of skill" on that target. Providing two successful demonstrations of skill earns the student a rating of "Fluent" on that target.

There's also a final exam, with a comprehensive portion and an optional second portion with last-chance quiz problems on all 20 targets. Otherwise, there aren't any other graded assessments.

The grading system

The Daily Prep assignments are basically graded pass/fail, but I am using points (0 points = fail, 1 = pass) to make things easier to understand for students. Everything else is graded Satisfactory or Unsatisfactory based on specifications that I have drafted but which aren't finalized yet (watch the GitHub repo, because finalizing those is next week's big task). The four-level EMRF/EMRN rubric is gone; I am taking my own advice to simplify, getting back to Linda Nilson's injuction to use only a two-level rubric, set the bar high for Satisfactory, and let the revision/resubmission process take care of the rest.

That revision process is also simple. You can't redo Daily Prep or the Final Exam, but you can revise and resubmit anything else that isn't Satisfactory, as much as needed, within certain basic boundaries. For example, Weekly Challenges can only be revised twice, and there are expiration dates past which Weekly Challenges can no longer be revised. (I don't want students waiting until week 13 to revise the Weekly Challenge from week 2.) And there is a special mark of Incomplete that can be given to a Weekly Challenge that is highly fragmentary and not a good-faith submission, where a token is required to revise it. But that's basically it.

All of this reflects my experience learning about ungrading and is sort of a first approximation to an ungraded version of this course. If a student does good-enough work on a Weekly Challenge or Learning Target, they get feedback to let them know it was good enough; otherwise they get feedback to let them know why it wasn't. Learning Target attempts will not list either the Satisfactory or Unsatisfactory labels, but rather a 0, 1, or 2 letting students know the number of successful demonstrations of skill they've produced. I'm trying to get away from using the gradebook as an audit of a student's goodness or badness, and more of just a place for factual information and leave the evaluative part of it for verbal feedback.

Here's how to earn a grade in the class, from the syllabus-in-progress:

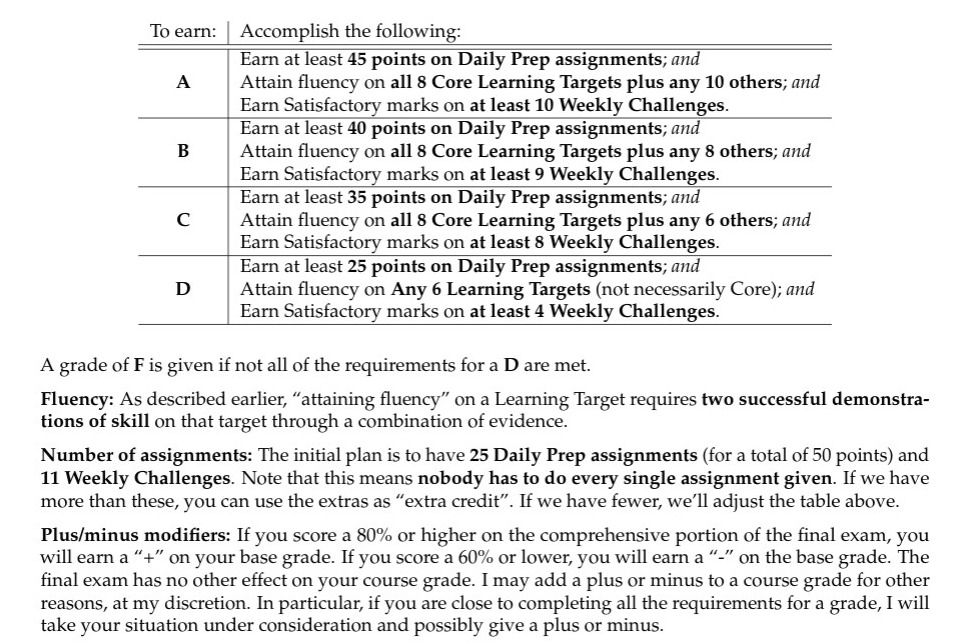
This feels like a major step in the right direction for my grading systems. The proliferation of multiple threads of assessment in the past led to grading systems that required argumentation that they were simple. If you have to convince a student that something is simple — it isn't. This actually is pretty simple. I was looking very much at my grading system for the second semester of this course back in Winter 2017, which I always felt was as good as I ever got it, and imitating it.

What I'm not sure about, or haven't done yet

• I am not sure if I'm going to keep the in-class pair worksheet part of the Daily Prep. I do want/need some second layer of assessment, something light and simple, on pre-class work to get students more fluent with the pre-class material for in-class work. But I'm not sure a quiz that takes place in the first 5 minutes of class is the best idea. Yesterday, I had an in-person meeting at our downtown campus and got stuck in traffic, and as I ran later and later, it brought home some of the practical issues with course assessments that depend on in-person attendance and precise timing. I'm kicking around ideas for alternatives.
• I want to incorporate some Agile principles in the course by getting systematic regular feedback from students. I've used the five-question summary before and will do that again, probably once every 2-3 weeks. But I'm also considering something like a sprint retrospective where we pause at the end of a "sprint", maybe at the end of each of the modules, and have an organized discussion about what went well and what could be improved. I'd love to set aside a class meeting for each of those and do them in person, but that's expensive. On the other hand, it's good intel, and CS students need to learn about Agile processes anyway.
• I haven't written the specifications for "Satisfactory" work yet. That's for next week, although I did something similar last year and I'll probably keep most of it.
• The syllabus isn't totally done yet. I will likely do one more round of edits on it next week then declare it to be done, so I can build out the rest of the first week, including a Startup assignment that usually involves a syllabus/calendar quiz on Blackboard.
• And of course there's the actual course planning. My goal has been to have the first week completely "in the can" by August 6 and I am on track to do that, then have the next three weeks more or less prepared by the start of classes, so I can stay 2-3 weeks ahead throughout the semester and be done with all the prep around Thanksgiving. I might not get there, but as long as the first week is done by the first week, I'll be OK.