Return to specs grading: Calculus

When I finished up my sabbatical in May, I turned my attention to two things: Shuttling my children back and forth to camps and sports practices, and trying to remember how to teach. I've gotten pretty good at the first of these. As for the second, we'll find out in two weeks, when for the first time in 15 months I will step back into the classroom as an instructor.

This Fall, I'm teaching a section of Calculus 1 and two sections of Modern Algebra 1. I started prepping these back in April, as the sabbatical was winding down, because I knew I would have a lot of rust and would need a solid 3-4 months not only to get back into the routine, but also find ways to make my teaching new and refreshed and not merely back into the old routines. The whole journey of rediscovering and reinventing my process for course design and preparation is worthy of another post. For now, I want to describe one particular aspect of my courses for this fall, namely the use of specifications grading in each of the courses I am teaching. I first wrote about specs grading three and a half years ago and have blogged about it off and on here as I've gone through several iterations in my classes. I also moderate a Google+ community on this subject^[1] and I can attest that there is a lot of interest in this alternative system of grading. In this post, I'll detail how I'm using specs grading in my hybrid Calculus section. In the follow-up, I'll write about how it's being used in Modern Algebra.

What is specifications grading?

Specifications ("specs") grading is a species of mastery grading which has been around for quite some time in various forms. Linda Nilson is credited with coining the phrase "specifications grading" and her book on this subject has much, much more about it; this article provides an accessible but detailed overview. My interview with Linda back in 2014 also has a lot of her insights.

Specs grading is based on the following principles:

• Student coursework is evaluated not using a point system but rather using a simple two-level (i.e. Pass/Fail) rubric, according to whether the work meets or exceeds predetermined criteria for quality. (Nilson suggests that "Passing" should be the equivalent of "B" level work, although this is up to the instructor.)
• Those criteria come in the form of clear, detailed specifications that are made public to the class (often fortified by examples of passing and non-passing work).
• Since there are no points, there is no partial credit. Instead, (most) student work is allowed multiple attempts, with non-passing work given extensive instructor feedback that students can use to improve what they turned in. Resubmissions are graded according to the specs and the grades updated if there's improvement.
• The students' course grades are still A/B/C/D/F, but determined by the quantity and quality of the work they turn in that meets the specifications --- not a statistical formula that combines points. The higher the grade, the more work and/or higher quality of work the student must supply as evidence.

I've been using specs grading since 2015, and it's revolutionized my teaching. It's not always easy and students sometimes push back; but it's absolutely a net win for all of us.

About the course

The section of Calculus I'm teaching has some distinguishing characteristics. First and foremost, it's a hybrid section, meeting twice a week (11:00-11:50 Mondays and Wednesdays) and the rest of the course is asynchronously online. The two F2F hours will be used only for active learning tasks and for assessment. The rest of the time, students will be engaging in reading and viewing, working out online activities, and practice. The vast majority of the course in other words is individual with just a touch of group time together.

The 26-ish students in the course^[2] are almost evenly split between first-year and third/fourth-year students, and there are a lot of engineers and a lot of biomedical sciences majors in the course. Most of the third/fourth year people are biomedical. So it's a mix of new students who are still emerging from high school; and grizzled veterans who are getting their last few courses out of the way before med school or grad school.

What students do

Here's the syllabus for the course which has all the details of the grading system. The grading system is on pages 3--6. What follows here is a summary.

Students do four different kinds of work:

• Guided Inquiry, which are structured assignments for students to use while learning new material on their own. We're a flipped learning environment, plus the course is hybrid, so students are doing most of the initial learning of concepts independently, and Guided Inquiry provides structure and guidance as students do this. Here's the first Guided Inquiry assignment in the course if you're interested. As you can see, each one contains text and video resources plus exercises that are submitted online prior to class. (I used to call these "Guided Practice"; I felt "Inquiry" better described these than "Practice".) Guided Inquiry is graded Satisfactory or Unsatisfactory on the basis of completeness, effort, and deadline-compliance only.
• The course also has 24 Learning Targets that spell out the main content objectives of the course. Ten of these are Core Learning Targets which are (in my view) things that every student who claims comptency in Calculus need to demonstrate they can do. The other 14 are Supplemental Learning Targets and are important but not (IMO) essential tasks. You can see the whole list of Learning Target in the syllabus in Appendix B. Students show their skill with these Learning Targets through in-class quizzes, which are graded Satisfactory or Progressing based on specs that are different for each target.
• Students also do online homework sets in the class which give them further practice with basics. We use WeBWorK for online homework; I am planning on two sets per week with 3-6 problems each. These are the only thing in the class graded with points because I can't make the system do otherwise, but it's essentially Pass/Fail because each problem is 1 point if correct, 0 otherwise.
• Finally, students do Labs, which are extended application problems involving computer technology. These are actually standard for all of my department's sections of Calculus and are a good way to assess student skill at extensions and applications. These are graded Excellent, Satisfactory, Progressing, or Incomplete. The two new levels here are for work that is truly outstanding, and work that has major gaps, omissions, or systemic errors that render evaluation impossible, respectively.

There is also a final exam that will be based heavily on Learning Target quizzes and will be graded with a sort of hybrid of points and specs. Also, I will be awarding Experience Points for doing things to engage with the class, like engage in online discussions or do something useful in a class meeting.

As is the case with specs grading, almost everything is redoable. Learning Target quizzes can be retaken during later quiz sessions, during a few designated quiz-only class meetings in the semester, and with any leftover time at the final exam session. Quizzes can also be retaken during office hours through 15-minute appointments. Labs can be redone through a take-home process described in the syllabus. WeBWorK sets can be redone as often as you want before the deadline. (Guided Inquiry assignments aren't redoable since they are for class preparation.)

How the grading system works

There are two parts to the determination of a grade: Finding the base grade (just the plain A/B/C/D/F with no plusses or minuses), and finding whether or not you have a plus or a minus on the base grade.

My belief is that the base grade should be determined and affected only by important stuff: Mastery of basic information, ability to extend and apply the basics, and preparing for class meetings. Other, not-as-important work --- such as the final exam^[3] and class participation --- should not affect the base grade but should be used to determine plus/minus modifiers.

You'll see that philosophy reflected in the requirements for each base grade, which are:

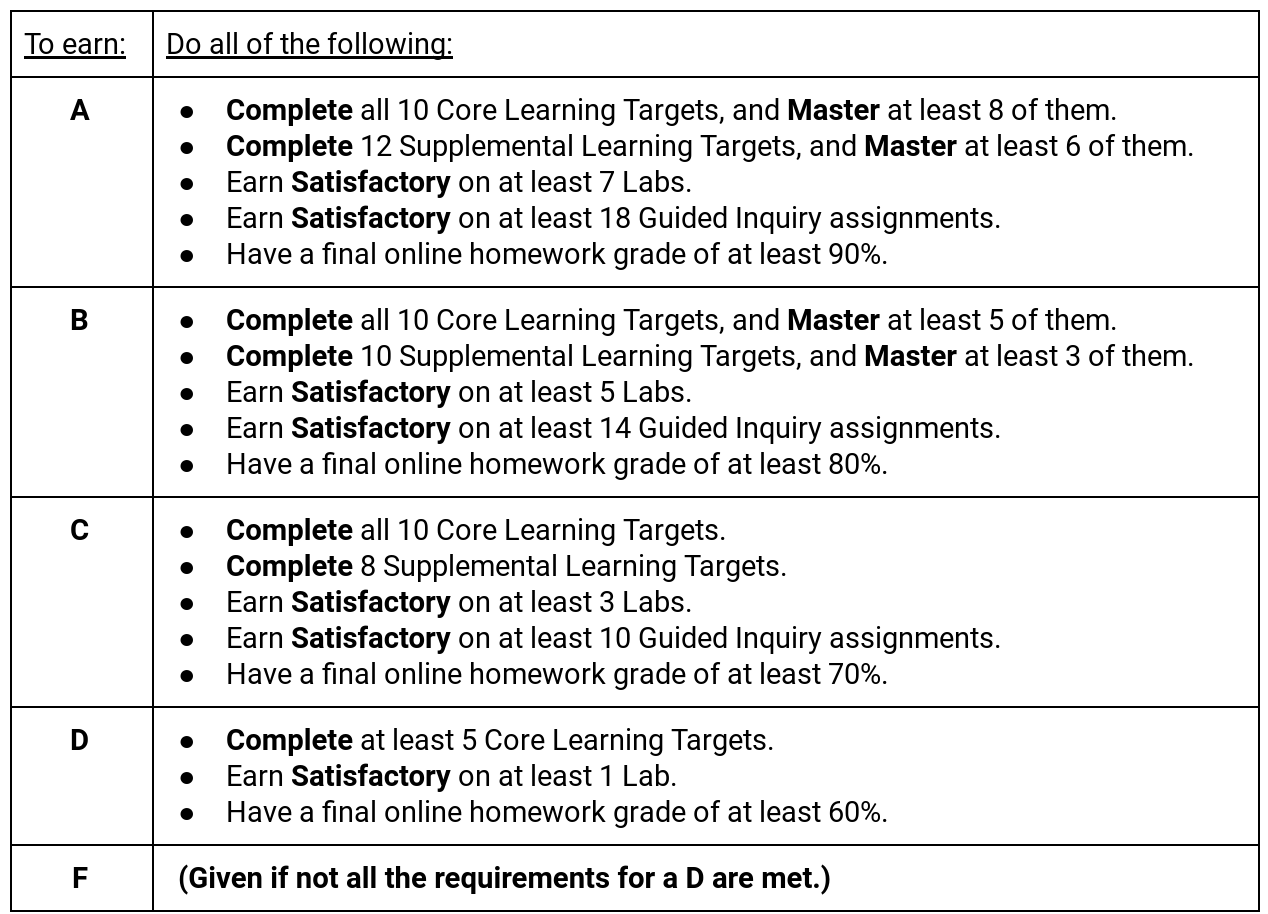
With Learning Targets, Completing a target means earning "Satisfactory" on one of the quizzes over that target. Mastering a target means earning "Satisfactory" on a second quiz over that target, which students can do during any time set aside for retaking Learning Target quizzes (of which there is a lot).

I built this table from the middle outward, by first asking: What does baseline competency in Calculus look like? That's what a "C" is. I happen to think my criteria for a "C" are very minimal almost to the point of feeling uncomfortable about it. But I decided that I'd err on the side of leniency rather than being too strict about it. For a B, students have to do more, and what they do has to be better than for a C. For an A, the same but moreso.

The base grade gets a + or - modifier depending on what happens with the final exam and XP:

• If the final exam grade is at least 85%, and at least 85 XP are earned, add a "+" to the base grade.
• If the final exam grade is less than or equal to 50%, or 50 XP or fewer are earned, add a "-" to the base grade.
• Otherwise the course grade equals the base grade.

So blowing it on the final, or willfully disengaging with the class (while still getting required work done) will not kill your grade, but it won't be without effects either. On the other hand, doing really well on the final and staying engaged with the class gives you a bonus, but not a massive boost.

What I like/don't like/am not sure about

What I like about this system:

• It checks all the boxes for me that specs grading normally does. Students have clear expectations and guidelines; it promotes a growth mindset; it's relatively simple in terms of the moving parts, and there's no mysterious statistical formulae to contend with; and it should shift the narrative on grades from "I need to make at least $x$ on the final to get $y$ in the class" to "I need to improve on Learning Target $n$".
• It fixes a bug with previous incarnations of my specs grading system where a student could demonstrate competency on a topic in one part of the semester and show evidence of non-competency later. Having students "Master" Learning Target with two points of data, plus having a final exam, gives more confidence.
• It all stems from a simple theory about grading, that grades should be based on basic mastery, ability to extend the basics, and staying engaged with the course. The "why" of this is easy to grasp and explain.

What I don't like:

• Like every specs grading system I have ever seen or tried, it still feels overly complex and forbidding to students. In my own mind, this makes perfect sense, but what about everyone else?
• There are steep dropoffs for not making some of the requirements. For example, if you complete everything for an "A" but have only 69% on online homework, your base grade isn't an A- or B --- it's a D! I tried building in more plus/minus rules to handle near misses like this but it made things unreadably complicated. I decided to leave things alone and instead make concerted efforts get students to understand that there are severe consequences for missing the requirements, and acceptable work in one area doesn't "average out" with unacceptable work in others. But I have a bad feeling that in December I'll be dealing with at least one student who didn't get the message, and thinks he earned an A- when in fact he has a D.

What I'm not sure about yet:

• I'm not sure whether I have budgeted enough time in the semester for in-class reassessment on Learning Target quizzes. I think so, but I fear we'll be in week 12 and half the class will have only completed half the Core targets, and then things get really scary. But in a hybrid class, it's difficult to know when/how to add more face-to-face time.
• I'm not sure what kinds of wild edge cases will show up where the grade doesn't reflect the student's work. On the flip side, I'm not sure if there are loopholes that students can game to get grades they didn't earn.

One final thing I will say about the complexity of specs grading systems: All grading systems are complicated. Some of them are just more open and transparent about it than others. In a traditional points-based system, when you see the table in the syllabus that says there are three tests each worth 25% of the grade and a final that is also 25%, it seems simple, but actually it isn't. It's just hiding the complexity: Figuring out what will be on the test, how the tests related to the course objectives (if there are any), how the composition of the final compares to the tests, and so on. There's a lot that students don't know and won't know until it's test time, and then it's one-and-done, and if you have a bad day or are a bad test-taker, you're screwed. With specs grading, it looks complex but that's because everything is laid bare and the student has complete control over all of it. This is a tough sell to students sometimes, but at least it's sellable.

In the next post, I'll go through the specs grading setup for Modern Algebra, which is a very different beast.