Building a specifications grading course, part 2

This is the second part of a two-parter where I am going into detail about how the grading system in my current course, Linear Algebra and Differential Equations, is set up. The first part, where I described the big picture of the course, its learning objectives, and what a "C" and "A" semester grade should mean, is here.
Today, we get into the weeds.
Assessments and marks
What will students do in the class, to demonstrate their progress toward the learning objectives I listed last time? It's complicated, because there are really three categories of learning outcomes that I'd like to see.
The first category is basic skills. These are tasks that you would typically find in the bottom one-third of Bloom's Taxonomy in the "Remember" and "Understand" regions:
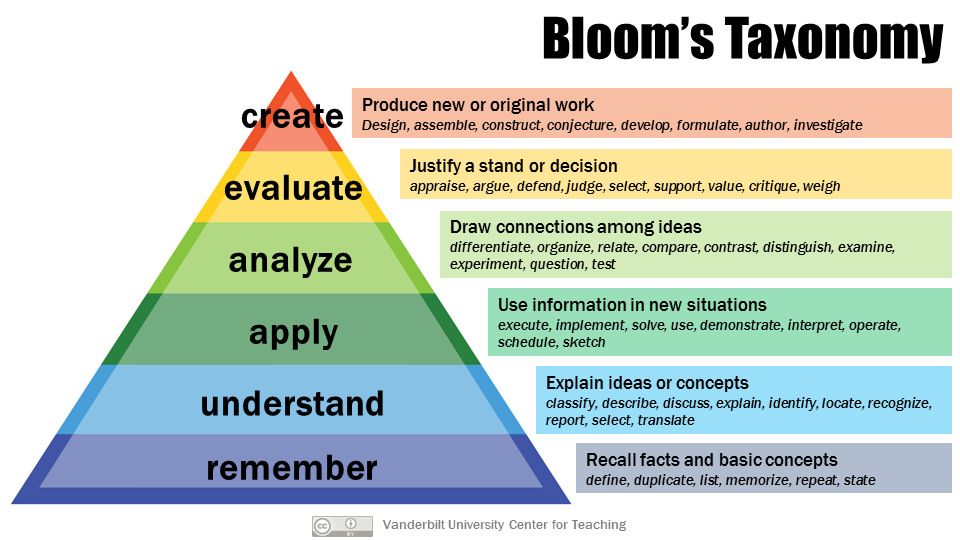
For MTH 302, this includes tasks like being able to state important theorems, identify the order of a differential equation, and explain why a set of vectors is linearly dependent or linearly independent. I also include in this category any kind of basic mechanical computation that is to be done outside of an applied context, things like multiplying matrices, computing a determinant, or solving a separable differential equation.
Students show progress on basic skills through doing weekly Practice Sets on our online homework system WeBWorK. I assign 5-10 Practice Set problems per week, each auto-graded by the software, worth 1 point each purely on the basis of whether the answer is correct. At this rate, we should end up with around 100 Practice problems by the end of the course.
We also have eleven Foundational Skills, which I mentioned last time and which you can find here in the syllabus. These are the core mechanical competencies in the course. Students demonstrate their skill on these through weekly Skill Quizzes. Each Foundational Skill appears on three consecutive quizzes, so at any given time there are between 2 and 4 problems on each quiz, each problem focused on one skill, with one Skill being introduced for the first time and others showing up again for those who need to retake them. Here is the second quiz of the semester and here is the third one. You can see that new versions of a problem are very similar to older versions, with the details changed. The "success criteria" at the end of each problem explain what "acceptable work" looks like.
Quiz problems are graded not using points, but instead are marked either Success or Retry. Note that this is for quiz problems, not the entire quiz. A student taking the third quiz above could have Success on Skill LA.2 but not on LA.3 for example. A problem is marked Success if it meets the success criteria. Otherwise the student retries it on a later quiz, and I'll say more about that momentarily.
The general setup I'm currently describing uses specifications grading. The actual specifications -- the overall criteria for what is acceptable work -- are in this document called "Standards for Student Work in MTH 302". The Standards document is sort of the Bible for our class (and for my grading) and students can use it as a "pre-flight checklist" for self-assessment before they turn something in.
The second category of learning outcomes is applications, or whether you know how to take the basic skills and put them to use in various ways. These kinds of skills are in the middle and upper thirds of Bloom's Taxonomy, and we have two kinds of assessments for these as well.
Miniprojects are the main vehicle for applications. As the name suggests, these are small but extensive project-like problems that require coding (using the SymPy package in Python), problem-solving, and written communication. There will be eight of these overall, and here is the first one. Miniprojects really aim for the top third of Bloom, "Evaluate" and "Create". Students do these in Jupyter notebooks using Google Colab, and they are marked Success, Retry, or Incomplete using specifications that are found in the Standards document. Each miniproject has some additional specs that need to be met that are unique to that assignment.
I used to stop here with my specs-graded courses and just have Foundational Skills, Miniprojects, and maybe some practice homework that's done on the computer and auto-graded. Over time, I've realized I was missing something, namely the middle third of Bloom's Taxonomy, "Apply" and "Analyze". So this semester I am debuting a class of assignments I am calling Application/Analysis, to fill in the gap between absolute basics and high-level applications.
Application/Analysis sets are turned in weekly and consist of specially designated activities that are part of our daily active learning activities. Students are working on things in groups most of the time in class, and some of those are being tagged for turn-in later. Here's an example; the entire handout is done in groups but the items tagged (AA) are turned in. Students are free to discuss them at length in their groups but when it's time to turn them in, they must do individual writeups. These are graded Success, Retry, or Incomplete on the basis of completeness, effort, and whether most of the work is basically correct. Some errors are allowed but if there gets to be too many of them, or they are particularly severe, I'll give feedback and mark the work Retry and the student can put in a revision.
The third and final category of learning outcome isn't really a learning outcome: Engagement. I don't really have a definition for this term (nobody does) but generally speaking I mean that students ought to be a living, breathing part of the course ecosystem. What it boils down to, for me, is whether students are preparing properly for class. (Work during class, is more or less measured by Application/Analysis.) Especially since this is a flipped learning model I'm using, I need students to engage with the pre-class work that I call Class Prep. These assignments, due the night before a class session, involve doing reading and video-watching, leaving questions and replies on these using Perusall, and completing a diagnostic quiz. These are marked Success or Incomplete based on completeness and effort only (not correctness).
Feedback loops
With the exception of Class Prep, each of these five buckets of assessments has a feedback loop attached that allows for feedback and revision.
- Practice Sets give immediate results about the correctness of an answer, and students can retry the problems unlimitedly until the due date.
- Application/Analysis sets get written feedback from me, and if it's marked Retry then the student gets one revision, due in one week's time.
- Foundational Skills, assessed on skill quizzes, appear on three consecutive quizzes. If a student's work is marked Retry then they take it again on a later quiz. If they try three times and never earn Success -- there is a Mega-Quiz at the end of the semester, an entire class period set aside for a quiz with all eleven Skills on it to give one "last chance" attempt to those who need it.
- Miniprojects marked Retry can be revised as often as needed. There is a limit of two miniproject items submitted per week --- two revisions, two new miniprojects, or one of each. These are posted whenever we have covered the necessary material to do them, and there's no deadline other than an initial due date by which first drafts must be submitted, and the last day of classes. The "two items per week" rule prevents students from dumping half a dozen miniprojects on me in the last week of classes. The initial due dates prevent students from submitting the first draft of an old miniproject late in the semester.
Class Prep doesn't have revisions or feedback because revisions don't work with pre-class assignments. The fact they are graded only on the basis of completeness and effort means revisions don't really matter anyway.
But otherwise, the assessment in the class resembles a busy beehive, with lots of small items continuously darting in and out of my and my students' inboxes, some new items and others that are older but being shaped through feedback and revision. As I've used specs grading, I've come to greatly prefer the "numerous but small" approach to assessments over the standard "few but large" approach (three tests and a final, for instance) and I think students do too, once they learn how to manage their information (more on that below).
Course grades
You'll notice that none of the assessments other than Practice problems have point values. Course grades are instead determined by tallying up how many Successes you have over the course of the semester. In the syllabus it looks like this:
| Grade | Total of Class Preps and Practice (100) | Application/Analysis (11) | Foundational Skills (11) | Miniprojects (8) |
|---|---|---|---|---|
| A | 85 | 9 | 10 | 5 |
| B | 75 | 7 | 9 | 3 |
| C | 65 | 5 | 8 | 1 |
| D | 40 | 2 | 4 | 0 |
I count each Success-ful Class Prep as one point, and pool them together with Practice Sets, to form what is basically an amalgamated "engagement score". If you're behind on Class Preps, you can do some more Practice problems; and vice versa.
Last time I described, in nontechnical terms, what a grade of "C" should look like: Basically minimum viable competency, the lowest possible level of achievement a student can have and be allowed to move on to the next course. I built the "C" row in this table with this description in mind, and I think what's there represents minimum viable competency in MTH 302. You could argue with the fact I only require one miniproject and you might be right.
For an A, I was shooting for excellence across the board and I think the requirements for an A capture this. Even so, I left a little room at the top so that I am not requiring anything like perfection from the A students. Everybody can simply punt on one Foundational Skill of their choice, for example. (This helps me avoid conundrums like when a student has maxed out all the achievements in the course but missed on one Foundational Skill.)
If it were up to me, I would only assign "whole" letter grades, but alas, I have to also have options for "plus" and "minus" grades. This is where the last kind of assessment comes in: the Final Exam. I've been moving away from giving final exams lately, but here I felt like they could serve a purpose, namely to be the primary method for determining plus/minus grades. Simply put: If you earn above an 85% on the comprehensive final exam, your basic grade from the table will have a "plus" added. If you earn below 50%, it gets a "minus". If it's in between 50% and 85%, the basic grade is unchanged. I like this approach: The final exam matters, but not too much, so students will study for it but hopefully not stress out about it.
There are also some provisions in the syllabus for earning a plus or minus on a grade if you partially complete requirements in the table rows. You can read those for yourself.
How it's going
During week 1, I took an hour of class time to train students on the grading system. They took a quiz on Blackboard (that didn't count toward their grade) where they were given hypothetical student accomplishments at the end of the semester, and they had to determine using the syllabus each student's grade. We also did a few of these in class and had discussions about the nuances.
For example, one of the situations involved a student who had "A" level work in everything but Miniprojects but "C" work in Miniprojects (i.e. they only turned in one or two of them with Success marks). That students' basic grade before plus/minus considerations is a "C", which counters students' intuition that stuff in a course should average together, with poor work in one area being balanced out by good work elsewhere. That's not how it works here: An "A" requires "A" level work in everything.
During that first week, the initial reactions to the system were mostly very positive, with students commenting along the lines of "finally, a grading system that actually allows me some room to grow". Some students were cautious about it, with some questions about the details of operations. But none of the students voiced anything negative, and they had plenty of anonymous chances to do so.
I've been checking in with students every few days to ask them how things are going in the class and if there are any things we should stop, start, or continue doing especially regarding the grading system. And in all honesty, I don't think students are really thinking about the grading system that much. There are still some misconceptions and questions about the details. But most of the time it just never really comes up. It's just sort of running as a background process.
One explanation for this is that more and more of my students' other professors are using similar systems. A lot of us in the Math Department do; and there are some great case studies popping up among the Computer Science, Physics, and Chemistry departments at my university as well. So this is not something totally unheard-of before by my students.
If I were doing this over again
So far, so good as we enter week 6 of a 15-week semester. But if I could go back and make changes:
- I'd allow alternative methods for showing proficiency on Foundational Skills -- not just quizzes but also oral quizzes in drop-in hours, or student-made videos. Some of my students freeze up when doing in-person quizzes and no amount of practice is ever going to change that.
- I'm not sure I would include Application/Analysis as I currently do it, by tagging selected group work problems for turn in. It's OK, but what tends to happen is that students go straight to those tagged items and spend the entire group work time working on those to the exclusion of all the others. I have to tell students "Please don't work only the AA problems" and it never works.
- These students are very high-performing, and although they are having few problems with the material they can sometimes be super grade-conscious. They don't have problems with my system; they just think about grades too much. So I wonder if I could or should have ungraded this course -- no graded work, just a portfolio for students to assemble through the semester that we discuss at the end for a collaborative grade. Maybe.
Thanks for reading all this! Again, you can follow the course's development through the stuff posted to the GitHub repository, and if you have questions for me, you can use the comment form on this website.


