Building a specifications grading course, part 1

In this recent letter to the ungrading community, I challenged ungraders to share their processes through consistent, honest blogging. Being transparent about what's working, what isn't working, and how you're adapting will clarify ideas in your mind and demystify them for everyone else. I never ask somebody to do something I'm unwilling to do myself, so in the same spirit, today I wanted to share my grading setup and initial experiences in the class I'm teaching now, where I am using specifications grading.

This started as a single article about the specifications grading system in the course I am teaching now. Pretty quickly it morphed into two articles that cover not only the grading system but all the background work it took to get a system in place that makes sense. As I describe below, I think this is the correct order in which to build a grading system. It's impossible to understand how grades work in a course without having some sense of the course background and learning objectives and this goes for alternatively-graded courses and traditionally-graded ones alike. Today, I'll describe my process for thinking about the context of the course and what role this plays, and how I determined the learning objectives for the course. Then next week, I'll get into the weeds about assessments and grades.

The course I am teaching is Linear Algebra and Differential Equations (MTH 302). It's a four-credit course primarily serving our School of Engineering, with nearly all of the 60 students across both sections being second- and third-year engineering majors. It hits the highlights of both subjects in the title, with an emphasis on the connections between them. I've taught linear algebra before, and differential equations before, but never this particular class with its hybrid point of view. I learned soon after I started building the course back in October that this course is different enough from past experiences that it requires fresh thinking.

You can find all the documentation for the course at its GitHub respository. In particular here is the syllabus, and I'll link to other documents in this post as needed.

The big picture

"Step 0" in the course build process, which I started back in October, is scoping the course: What's its purpose? Who takes it? How does it fit into the larger curriculum? I noted some of those situational factors above. Especially important is that this is a math course for engineers and the engineering school, which to me implies a particular approach to the subject matter: heavy on the applications and connections between concepts, a light touch with the theory, and a central role for technology.

Starting from here, I skimmed the entire textbook and wrote down all the things that I think students would learn, going section by section using the university's syllabus of record to tell me what we should and should not cover. From that list, a "module" structure for the course began to emerge organically around which I could build the particular learning objectives, and from there the system for assessment and grading.

That big-picture view also helped me frame the "motto" for the course, a single easy-to-remember message for what the class is about. I settled on:

MTH 302 is about systems, how we can model systems, and what we can learn about systems from the models.

The notion of systems as the central organizing principle really fits well. We start off with linear algebra, which is about systems of linear equations. Then we move to differential equations, which are also a kind of system where a function and one or more of its derivatives are intertwined. Then, the centerpiece of the course is systems of differential equations -- systems of systems -- where the two subjects in the class come together. Since engineers are all about systems, this emphasis not only neatly summarizes the course but does so in a way that's compelling to the students.

It didn't hurt that I'm studying systems thinking as part of my ongoing leadership development and work in the President's Office. In fact shortly after I had finished the initial build of this course, I read this overview of systems thinking that reinforced my course design and gave me some ideas of new concepts about systems to include in the class.

Keeping the end in mind

In our forthcoming book, David Clark and I suggest that once you have a course outlined and scoped, a good step toward building a grading system is to take the course grades of C and A, and write a narrative description for what those should look like -- not in terms of specific assessments or grades, but as a general overall description that would make sense to an outsider. Here's what I settled on:

In MTH 302, a grade of C means: There is evidence of skill on all the fundamental, can't-live-without-it ideas and at least minimal success with applying those basic ideas to real problems. And, the student has participated and prepared meaningfully more often than not. Basically a "C" student is good to go with the bottom one-third of Bloom's Taxonomy, has made at least a little headway in the middle third, and they've given a good faith effort to be part of the learning community in the class.

In MTH 302, a grade of A means: The student has mastered all the fundamental ideas and has a pattern of success in applying those to authentic problems involving modeling systems. An "A" student also shows consistent engagement with practice and preparation for class. They have mastered the bottom two-thirds of Bloom's Taxonomy and have evidence of consistent success with the top third.

This is what "minimal viable progress" and "excellence", respectively, look like to me. In case you aren't familiar with Bloom's Taxonomy, this picture is pretty self-explanatory:

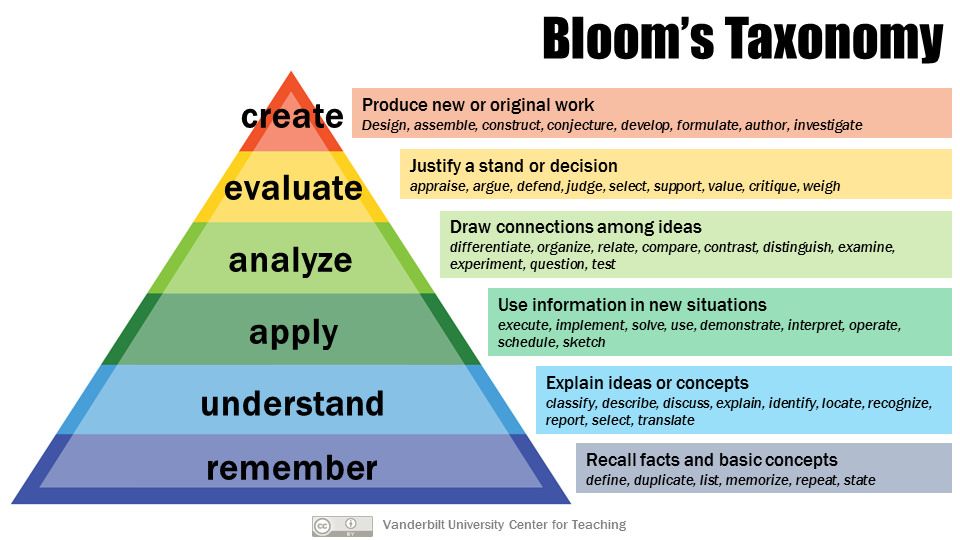
I wrote a little more in this post about how viewing Bloom's Taxonomy in thirds helps with course design.

A tale of two lists

Once I had clarity on the context and overall story arc of the course, and what "minimal competency" and "excellence" looked like, the next steps were to flesh out the learning objectives in the course and decide what students would do to demonstrate skill on them, and how those would be assessed.

Before I say more about that, note that the ordering of the steps in this process matters. What many faculty do, and what I definitely used to do, in building a course is to start with the assessments (how many tests, how often homework is turned in, etc.) and then write up the grading system, and give little attention to learning objectives in the course or what the course is about. I've found that what the course ends up being about, in the end, is grades. If you lead with grades, and just assume that the meaning of the subject and the specific skills attained in learning it will just sort of "happen" along the way, then you can't really expect students to pay attention to anything but their grades. Given how common this approach to course design is, and how demoralizing traditional grading can be, it's no wonder so many students and faculty are burned out and exhausted.

Back to MTH 302: I had already made a long list with all of the micro-scale learning objectives for the entire scope of the course when I reviewed the textbook. I put those into a long note:

And on and on this note went. It's a list of all the ideas and tasks that students would encounter. It was not a list of things that I assess! This list was like a list of all the things you see on the road when you drive from one city to another. But it is not a list of directions of things you must do, to make that drive. I'd realized before that not every idea that students learn in a course rises to the level of needing to be assessed. Indeed it is not humanly possible to assess every single thing that a student has encountered in a course to see if they learned it. Instead, the big list above was a guide for lesson planning; and I used it to isolate the truly central learning objectives that I would eventually assess.

You can see some of those "assessable objectives" in my list, in bold-face (for example "Add, subtract, and multiply matrices"). At this stage my goal was to filter the list of "things to learn" down to a minimal number of assessable learning objectives that fits my vision for the course. There were lose to 100 micro-scale objectives in the big list. I filtered this down to twelve central objectives:

And before it was all over, I ended up dropping the last one about Laplace transforms, ending with eleven Foundational Skills. (I really wanted to get down to ten, but I couldn't justify cutting any more to myself.)  

The Foundational Skills are the "bottom third of Bloom's Taxonomy" that I referenced in my narrative about what a "C" and "A" look like. They form the basis for everything else students do in the course. Students will be doing more than just demonstrating skill on these; for example I said that both C and A students should show evidence of being able to apply these skills to real-life problems. But all of those applications come from these.

If you happen to know linear algebra or differential equations, you might wonder about some of the skills not on this list. What about determinants? Slope fields? And why did you get rid of Laplace transforms? To be clear – I didn't "get rid" of these topics. They are there, and we'll encounter them. But for this class and these students, I consider them not to rise to the level of needing explicit assessment.

Most of the topics that didn't make the final cut, are calculations that are best done on a computer. Here in 2023, with a superabundance of free computer tools that will compute determinants and generate slope fields quickly and flawlessly, I see no reason to task students with doing these by hand when we could use that time and energy to learn how to use the concepts to model systems and learn what we can from the models. So next week, we're going to spend about 15 minutes practicing finding the determinant of a 2x2 and 3x3 matrix to get the gist about how it works; and then we will never do it again but instead use SymPy to find determinants for us.

You could make the case that there are Foundational Skills on this list that can and should be treated similarly, for example generating numerical solutions to first-order DE's, a process clearly best suited for a computer. My take is that there are some tasks that, while best suited for a computer in actual practice, are worth the time and effort needed to do by hand, on a small scale, to learn how the algorithm for the task works. When I teach computer science majors about big-O analysis of algorithms, for example, I have them act out a sorting algorithm by sorting a stack of paper cards with numbers on them using one of the algorithms. This is unlikely to ever happen in real life; but when you do merge sort on a stack of 8 cards, then 16, then 32, you internalize what $O(n \log n)$ really feels like.

Likewise, I think running Euler's method on a small scale helps you internalize what the computer is doing and what the result allows you to do. Finding determinants of 3x3 matrices, on the other hand, doesn't seem to me like it provides the same level of return on investment. Definitely not 4x4 matrices! And, I might feel differently if it was another course with another demographic of students. For a crowd of computer science majors, doing a 5x5 determinant might be useful for getting a feel of the recursion in the process. With engineers, we probably have better things to do.

Also, I made a scientific poll of practicing engineers — OK, it was my sister and my two brothers-in-law over Christmas break, but at least they are real engineers — about the last time they ever had to compute a determinant or make a slope field by hand in each of their 30+ year careers as professional engineers. The unanimous answer was "Never". I'm not into making students do what amounts to fancy nerd party tricks just so I can say that we did them.

Getting there

Next up is the system for assessing whether students are learning the things I want them to learn, as well as the feedback loops in place for helping them grow, and how all of this fits together into a course grade. With all of the above in place, these bits can now make sense — but not before! We'll get into all that next week.