Re-thinking Bloom's Taxonomy for flipped learning design
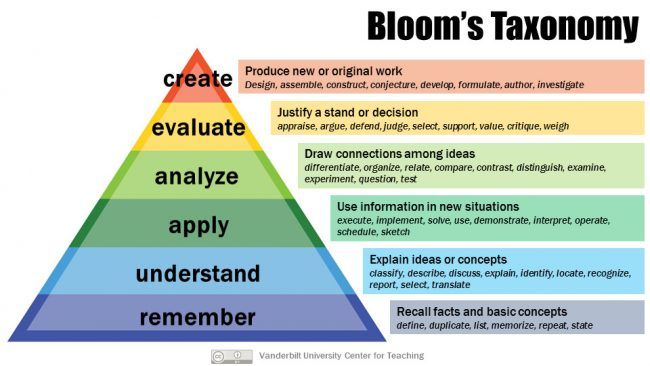
Most instructors are at least a little familiar with Bloom's Taxonomy, which is usually depicted as a pyramid:
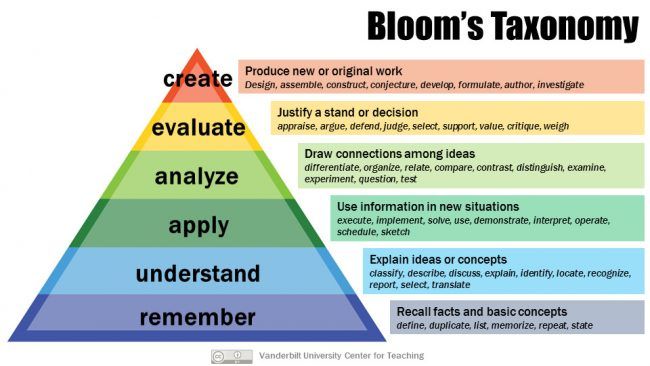
Bloom's Taxonomy is a way of categorizing cognitive tasks in terms of their difficulty or complexity. It is most definitely old-school, invented by Benjamin Bloom in the 1950's and updated in the 2000's. The taxonomy in the pyramid above is actually just one of three parts to Bloom's Taxonomy, the other two addressing affective and psychomotor skills. It's a handy diagrammatic way of thinking about how "hard" different kinds of learning tasks are, and how they (literally) stack up against each other. And it should be stressed that Bloom's Taxonomy is just that: A taxonomy, a naming system, and nothing more. It's not a heirarchy that suggests that the lower levels are less important than the upper ones; nor is it a timeline that insists that one level must be mastered by learners before moving on to the next level.
I've used Bloom's Taxonomy countless times in talks, workshops, my book, and in my teaching practice to think about how to sequence learning activities, especially with flipped learning. Specifically: In traditional lecture-based instruction, we assume that learners encounter new ideas for the first time in their group meetings, where we assume they have zero knowledge of the new topic and focus class time on the bottom half of Bloom's Taxonomy. And then students work out the more complicated extensions of that basic knowledge, the upper half of Bloom's Taxonomy, through work done after class (homework, projects, etc.).
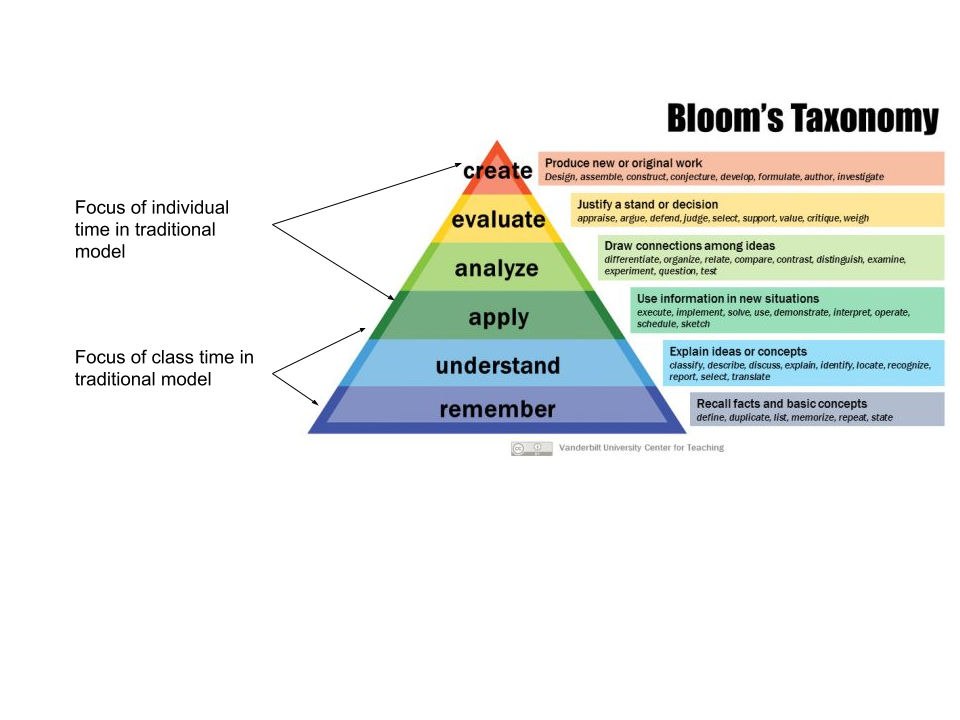
This model, with its emphasis on spending class time exclusively on the bottom 1/2 of Bloom, has numerous issues which I describe at length in my book. The foremost of those issues is that it aligns the difficulty of student work inversely with student access to help --- learners hit the hardest material when the instructor is least available and group collaboration is possibly outlawed by the syllabus. Traditional instruction also fails to take advantage of opportunities to help students become self-sufficient learners, because the material most amenable to self-teaching --- the bottom half of Bloom --- is co-opted by the instructor.
Flipped learning, on the other hand, literally inverts the focus in terms of Bloom's taxonomy, so that the bottom parts of Bloom are reserved for student self-instruction through structured activities, and class time is focused on the upper parts of the taxonomy --- the most complex tasks, which are best served by having a rich social environment in which to work (i.e. class time).
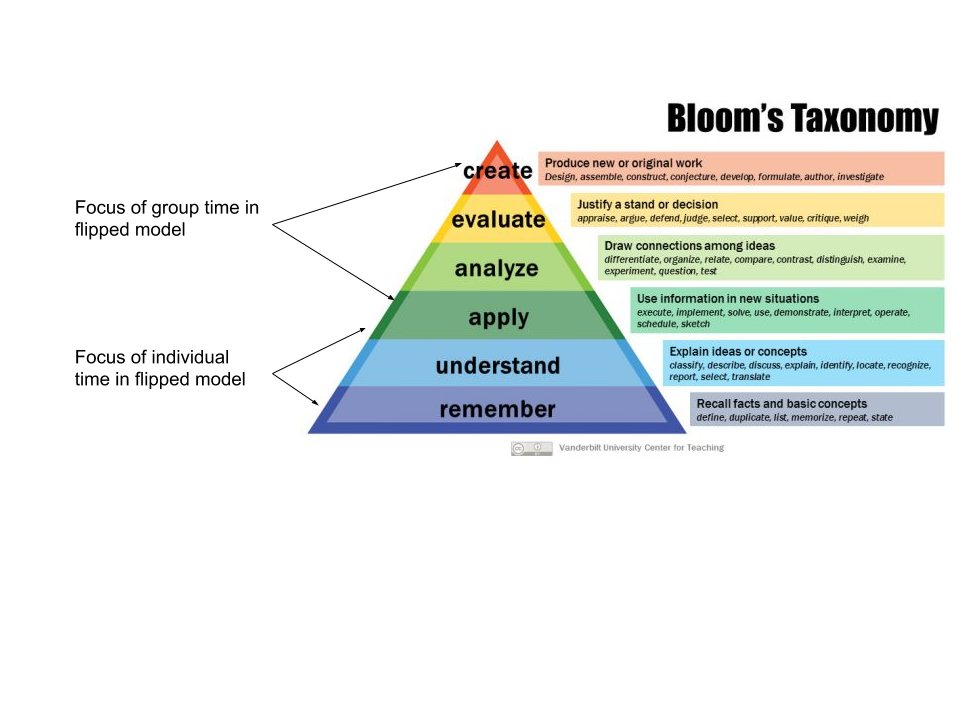
Framing flipped learning in terms of Bloom's Taxonomy has, for me and the people in my workshops and talks, been a helpful way to visualize the concept. But recently, while preparing for a webinar on time management in flipped learning, I took this a step further, and I think the result has even better explanatory power.
Traditional instruction still assumes zero knowledge of new topics coming into class, and then the class meeting focuses on the bottom half of Bloom and post-class work on the upper half. But in applying Bloom's Taxonomy to flipped instruction, rather than just flipping the halves, it's more helpful to break Bloom's Taxonomy up into thirds.
- Pre-class work in flipped learning focuses on the bottom 1/3 of Bloom's Taxonomy, that is, tasks related to "remembering" and "understanding". We insist students learn these tasks on their own prior to class through structured activities.
- In-class work then picks up where the pre-class work ends, focusing on the middle 1/3 of Bloom, that is, tasks related to "applying" and "analyzing". These are the simplest extensions of the basics and will be the place where students need the most immediate help.
- Post-class work uses the basics and the extensions to address the top 1/3 of Bloom, that is, tasks related to "evaluating" and "creating". These are the most complex tasks students can perform with a topic, and they often do not fit neatly into a 50- or 75-minute class period and are thus not good targets for using class time (although parts of those tasks can be addressed).
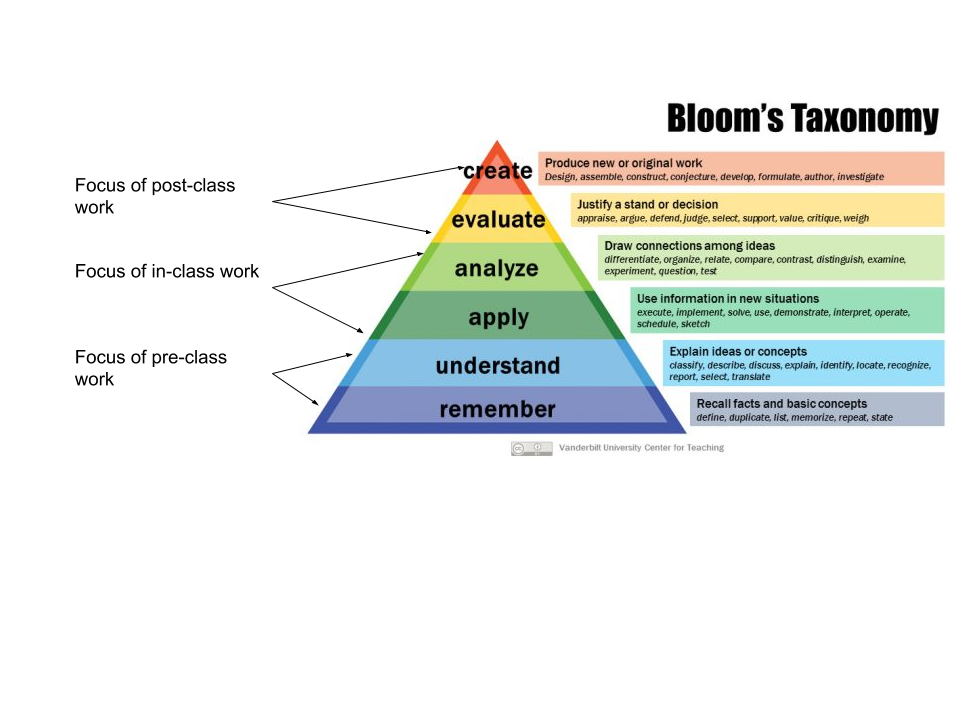
This division of labor seems to accomplish at least three important things for flipped learning:
- There are "cleaner edges" on the three phases of student work (pre-class, in-class, post-class) and therefore more focus and more perspective on what we should be doing in those phases. For example, thinking of learning activities in this way, we'd avoid putting tasks from the middle or top third of the taxonomy into students' pre-class assignments because this would be too difficult for many students and would steal energy better suited for mastering tasks in the lower third. Likewise, we'd steer clear of spending class time on tasks in the lower third of the taxonomy --- for example, giving students worksheets to do in class that merely rehearse rather than extend the basics --- because the basics have already been covered and now we need to spend time extending them.
- Students will be clearer on what they are responsible for learning prior to class and what they are not responsible for. Students need to be told what not to do just as much as what to do in order to focus their limited energy and time on the right things.
- By having the division of tasks like this, time management both outside and inside class meetings becomes easier. When you know that your class meeting should be focused only (or at least overwhelmingly) on application and analysis tasks, and not on basics or very-high-level tasks, there's less of a temptation to write a class activity that tries to do both, and so there's less opportunity to waste time on tasks that are inappropriate for the moment.
I'm teaching our "Functions and Models" course (a 5-credit course for students preparing for calculus) this summer and next year. It uses Matt Boelkins' free textbook. Here's what this split-into-thirds concept might look like as I prepare the lesson for Section 1.5, Quadratic Functions.
First, according to my Seven Steps philosophy, I'd come up with a list of learning objectives for the lesson and then reorder them in terms of Bloom's Taxonomy (simplest first). Here's a possible take on that reordered list, with the objectives that map into the lower third of Bloom ("Remember" and "Understand") highlighted:
- State the definition of a quadratic function.
- Define what it means for a function to be concave up or concave down on an interval.
- Write a quadratic function in vertex form.
- Find the coordinates for the vertex of a parabola given by the quadratic function $f(x)=ax^2+bx+c$.
- Use the quadratic formula to find solutions to the equation $ax^2=bx+c=0$.
- Given a quadratic function $f(x)=ax^2+bx+c$, explain the effects of each of the parameters a, b, and c on the shape of its graph.
- State whether a quadratic function is concave up or concave down.
- Find the average rate of change in a quadratic function over an interval.
- Explain the specific behavior of the average rate of change in a quadratic function over equally-sized intervals.
- Apply basic computations involving quadratic functions in real-world problems.
- Given a data set, determine whether the data follow a quadratic pattern and if so, fit a quadratic function to the data.
Assuming that this is correct for my situation, those seven items would be the sole focus of students' preclass work. I'd want to make sure that each of those objectives has at least one of the exercises I give students before class focused on it. These basic objectives are all things that students can, and should, be learning on their own through structured activities. To teach them for the first time in class is to misuse the class time and rob students of the opportunity to build their autodidactic skills.
Of the four remaining objectives, I'd say the first three are middle-third tasks ("Apply" and "Analyze") --- definitely the first two are, and the third (applying to real world problems) could involve simple applications in class and more complex ones later. So those three items are the sole focus of in-class work. We will not spend time in class on any other objectives, except maybe a recall activity in the first 5 minutes of class to jog students' memory of the basics --- because those basics have already been covered, by students in their pre-class time. My in-class activity should then have an item about finding average rates of change and discovering that the average rates on equally-sized intervals change at a constant rate, plus some basic applications to real world problems.
Finally, the last objective (modeling with a quadratic) is something I would leave for post-class activity, mostly because it involves using (and therefore learning) technology for doing this and perhaps gathering authentic data to analyze. That's a worthy goal, and it needs more time and space than my class seswill allow.
In terms of my Seven Steps process, I would split those learning objectives into "Basic" and "Advanced". Under this rubric, the Basic Objectives would be the ones targeting the bottom third of Bloom and the Advanced Objectives are everything else. In the pre-class assignment, it would all come together to look like this:
BASIC objectives: Each student will be responsible for learning and demonstrating proficiency in the following objectives prior to the class meeting:
- State the definition of a quadratic function.
- Define what it means for a function to be concave up or concave down on an interval.
- Write a quadratic function in vertex form.
- Find the coordinates for the vertex of a parabola given by the quadratic function $f(x)=ax^2+bx+c$.
- Use the quadratic formula to find solutions to the equation $ax^2+bx+c=0$.
- Given a quadratic function $f(x)=ax^2+bx+c$, explain the effects of each of the parameters a, b, and c on the shape of its graph.
- State whether a quadratic function is concave up or concave down.
ADVANCED objectives: The following objectives should be mastered by each student DURING and FOLLOWING the class session through active work and practice:
- Find the average rate of change in a quadratic function over an interval.
- Explain the specific behavior of the average rate of change in a quadratic function over equally-sized intervals.
- Apply basic computations involving quadratic functions in real-world problems.
- Given a data set, determine whether the data follow a quadratic pattern and if so, fit a quadratic function to the data.
Long story short, I'm liking this way of splitting Bloom's Taxonomy into thirds and using these as a tool for sequencing learning activities in a flipped environment. It helps give both focus and perspective to our work and our students' work, which saves time and makes that work more effective.