Building Calculus: Learning objectives

As of today, there are 53 days until the start of Fall semester at my university, and every weekday I am building my classes – two sections of Calculus and one of Discrete Structures – just a little more. And as promised, I will be sharing my processes and the results-in-progress as they get built. In the last post on this topic, I shared my thought process for choosing the "staggered hybrid asynchronous" approach to the course. Since then, I've been spending most of my time working on the heart of the Calculus course: the learning objectives.

I think those are in a stable-enough state that I can share those now. But first, I wanted to mention that I'm making all my notes and materials are publicly available on GitHub. There are two repositories:

• Calculus: https://github.com/RobertTalbert/calculus
• Discrete Structures for Computer Science: https://github.com/RobertTalbert/discretecs

Fair warning: Right now (July 9) these repos resemble junk drawers because I'm still roughing things out. But in the next few weeks I think I'll have things put together to the point I can invest time in organizing them. But at any rate, all of this stuff is free for you to use, steal, fork, etc. to your heart's desire.

Why learning objectives are worth the time

I've written a lot about the importance of learning objectives. Most recently, I wrote about how having clear, measurable learning objectives is the essential first step in a well-designed online course. This is because I am eventually going to design my learning activities so they align with those objectives and do the same for my assessments, and even use the learning objectives to guide my selection of course materials and technological tools.  

These are decisions to make in sequence, not in parallel, and learning objectives are the first step. Often in the past, I'd start building a course by deciding what kind of graded work students are going to do, what the textbook is going to be, and what material I'm going to cover, as more or less independent choices. But I've come to realize that's a mistake. I first have to decide what I want students to be able to do as a result of their experiences in the course, then work backwards to pick the right content, the right learning activities, the right assessments, and the right tools.

Course level objectives

There are two levels of learning objectives to consider:

• Course level objectives (CLOs): These are the global, overarching "big picture" items that students should master as a result of taking the course.
• Module level objectives (MLOs): These are finer-grained objectives focused on specific content tasks, connected to specific units or "modules" of the course.

Both sets of objectives need to be clear and measurable (as explained in this post). If you don't like "measurable", substitute "observable". What we don't want are objectives that aren't clear from the students' standpoint or which cannot be directly observed, like anything using the verbs "know", "understand", or "appreciate".

Writing the CLOs for the Calculus course was harder than I expected for two reasons. First, it's really hard to avoid "know", "understand", and "appreciate" when writing big-picture objectives. Second, we have a standardized set of course objectives that the department wrote some years ago (click here for direct access):

These are weirdly written – they start with definite integrals and then eventually get to derivatives, which is the opposite order in which the concepts are learned – and there's a couple of "know"/"understand" type objectives there. But this is sort of the law of the land in the department, and I need to ensure these objectives are met.

So job #1 for me was to remix these objectives and state them in a way and an order that makes sense, and which is both clear and measurable. Here's what I came up with:

I opted not to include in the CLOs things that were process-oriented, like Use technology to frame and solve mathematical problems or Demonstrate the ability to learn from feedback. Those are definitely things we will stress, and I want students to be able to do them. But I wanted to keep the CLOs brief and focused. And especially, whenever I write a learning objective, I am also making a commitment to assess that objective at some point. Otherwise it's disingenuous to put the objective on the list. At one point I had some technology-oriented CLO on the list but then realized that as currently structured, it didn't make sense in the course to make a way to assess it, so I struck it from the list.

This may change as the course evolves, and you don't have to do exactly what I do. Just realize that every time you write a learning objective you are also making a commitment to providing a learning activity for students to practice it and a means of assessing it. If you can't follow through with that, drop the objective. Don't write checks that your pedagogy can't cash.

Modules

With the course-level objectives in place, we can now think about the module-level objectives. Except first, I have to think about the modules themselves. Chunking your course into thematically-focused modules is a best practice in online teaching, because it provides a boundary inside which various learning activities, materials, and assessments can be contained. And that's good for students, because giving learners a pre-built structure that breaks up the course into manageable pieces helps reduce cognitive load and focus attention, both of which are critical for online learners (particularly the most vulnerable ones).

I've always liked breaking my online and hybrid courses into modules that last about one calendar week, because it sets up a nice predictable rhythm where most things happen at the same relative time; then I map the course content into the modules. Our Fall semester starts Monday, August 31 and ends on Friday, December 10. In between we have recesses on September 7, October 26-27, and November 25-26. I opted to take the first two days of classes (August 31-September 1) as a welcome/startup meeting; and I designated the last week of classes (December 7-10) as a catch-up week with no new content. I was able to fit 12 modules of five weekdays each very neatly into what was left over, with most modules covering two sections of our textbook (Active Calculus by my colleague Matt Boelkins).

After some experimentation with what should go in each module, I came up with this list:

I like phrasing each module as a question to be answered, so at the end of the module I can ask students to answer it, e.g. So, how do we find the speed of a moving object?

A few details about these modules for the math people in the audience:

• Module 3 is a bit dense, but Section 1.8 (L'Hospital's Rule) is going to be done as an independent student project later in the course, not as part of the regular class flow.
• Modules 8 and 12 are just one section, because the sections (Applied Optimization and the Fundamental Theorem of Calculus) are super-dense and historically difficult for students.
• Module 9 has an unusual grouping of sections, but I always felt that implicit differentiation (2.7) is best framed as a prelude to related rates problems (3.5) rather than as an application of the Chain Rule (2.6).

Again, this might change (it's already been overhauled twice since July 1) and your mileage may vary. The important thing here is to make sure you're breaking the course into modules in the first place and that the organization of those modules is consistent and makes sense.

Module-level objectives

OK, now we can think about module-level objectives. In addition to being clear and measurable, my MLOs have to align with the CLOs. This basically means that every MLO that I write should flow into one or more of the CLOs, like a tributary creek that flows into a river that eventually empties out into the ocean. An MLO that doesn't fit with the CLOs needs to be reframed or dropped. And the connection between individual MLOs and the CLOs needs to be explicit and clear.

The reason this is important is that students will be asking Why are we learning this? – at least we hope that they are asking that question – and having a clear connection from any point "on the ground" in the course to the big-picture course objectives will make it easy to answer that question and therefore keep students motivated.

I began the process of writing out MLOs by going section-by-section in the Active Calculus book and writing out every task that students should be able to perform after completing the section. Here's the list I came up with – not embedding that this time because it has 68 separate items on it by my count. And that was a problem, because as I said above, whenever we include an objective on an official list we are also making a commitment to assess it at some point. The thought of assessing 68 individual points of skill, and keeping track of student progress toward mastery of those items across two sections of the course, just made me tired.

So I decided to look through the list and group together related tasks into a shorter list of module objectives, while looking ahead at the assessment and grading scheme I wanted to set up. Everyone who knows me or this website knows my commitment to mastery (aka specifications) grading. And as I detailed here, mastery grading entails the use of what I call "learning targets" that represent important specific skills that students will need to master. After thinking about how mastery grading will work in this course, and after some experimentation with the list, I decided that the learning targets I will eventually assess will be my module-level objectives.

The way I thought about it was like this: The CLOs are your big-picture items. The MLOs are the finer-grained content tasks directly connected to the CLOs, and those will be assessed through graded work. The CLO's on the other hand are assessed not directly but indirectly through mastery of the MLOs. And the super-fine grained objectives from my list of 68 – I started calling them "micro-objectives" – are also not directly assessed but are incremental steps along the way to mastering the MLOs.

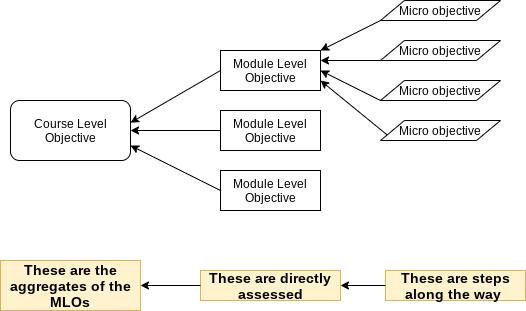
With this in mind, I was able to come up with a list of 24 Learning Targets/module-level objectives for the course:

The list originally was closer to 30, but keeping in mind that I will be assessing any learning objective I officially publish, and also keeping in mind that I hate grading, I took pains to remove or consolidate several of my original targets to get the list as short as possible.

Some of these are designated as Core targets. I'll explain more about that when I post about the grading system, but basically these 10 targets are what I consider essential knowledge for Calculus, and a student must demonstrate mastery of these in order to be eligible for a grade of C or higher.

Linking the objectives

Note that the MLOs/learning targets are (I think) clearly stated and measurable. I like to phrase them in the form of "I can..." to get students thinking about what they can do rather than what they can't do.

To make the connection between the MLOs and CLOs clear, I introduced a simple naming system that encodes the relationship by giving each CLO a one- or two-letter identifier; for example the CLO Calculate, use, and explain the concept of limits was designated L (for limits), and the CLO Use derivatives to solve authentic real-life application problems was designated DA (Derivative applications). Then, the MLOs are given a designation that includes the CLO they are connected to along with a number. Here's the above list, remixed and renamed in this way:

So now, there's a clear way to see how each learning target connects to the big picture. To see how each "micro-objective" connects to each learning target, I'll be doing that in students' individual pre-class assignments – I'll post examples when I get to that point.

There was one final link that I wanted to see: Where each learning target appeared in the course. I knew how each one connected to a CLO, but how did they connect to the sections in the textbook? I went through each learning target and each section of the book and made this nifty course map.

This revealed a few things I didn't already see. First, one learning target (DC.2) extends across two different modules; I'll need to think later how the assessment will work there. Second, Module 12 at the very end of the course is stacked with learning targets, so I'll need to take care and provide extra support when we get there – and also think about alternative assessments, since there's only two weeks left in the course when we start that module.

Summing up

I put a lot of effort into the learning objectives for a course because if you get those right, and give yourself a strong structure at the beginning, it makes a lot of things 10x easier later. For example when dealing with the difficult question of What should I have students do during the face-to-face meetings if we're socially distanced? the answer is: What learning objectives will they be working toward? The answer acts as a filter that focuses pedagogical choices down to only those that are truly relevant. On the other hand, if I don't give these due attention, I'll likely end up duplicating effort later or waste a lot of time and energy on the wrong questions.

I also often geek out and go overboard with this, so if you feel overwhelmed by the above, here's the basic gist:

1. Write out clear, measurable/observable course level objectives first – the big-picture items that successful students will be able to do as a result of their experiences in the course. Keep in mind that introducing a learning objective commits you to providing practice and assessment on that objective, so don't go crazy here. Keep it brief and focused.
2. Break the course down into smaller modules that have a coherent narrative or topical focus. (This can be done first if desired.)
3. For each module, determine a short list of module level objectives that are also clear and measurable that represent fine-grained atomic-level tasks – but not too atomic. Remember: Brief and focused.
4. Make the alignment between the module level objectives and the course level objectives clear. Use a nomenclature system like I did, or a concept map, or a bulleted list, etc.

Also, be prepared to revise your learning objectives as you build the course. You are allowed to change your mind and probably will do so. But not forever, because we need a stable, final list of learning objectives to move on to the next phase of building – which is about learning activities. Details on how that's shaping up for calculus, next time.

MY PERSONAL CHALLENGE TO YOU: Take one of your courses for Fall semester and focus for the next 3-4 days on creating the course- and module-level objectives for it. Put those in a public place and share the link in the comments.