Ungrading after 11 weeks

Last semester, when I learned I would be teaching Modern Algebra --- a third-year level course on number theory, rings, and fields --- in January, I knew I wanted to make some changes to how I'd taught it in the past. I wrote about that in my previous post. One of the changes I decided to make was to make a full-throated leap into ungrading. And I wrote about that here.

Now that it's week 11 and we're starting to put the landing gear down on this semester, I wanted to report back on how it's gone --- the good, the not-as-good, and observations I've made about ungrading in general.

What is ungrading and what possessed me to try it

Ungrading is a concept that has stubbornly resisted definition, but here's my take:

It is a form of "grading" in which students still do work, and that work is aligned with clearly defined learning standards. But, none of the work gets a grade, or as non-Americans would say a "mark". Instead of a mark, the work is carefully evaluated and gets lots of helpful feedback, and there is a feedback loop system in place whereby students can revise and resubmit, and get more feedback, and so on until the work is deemed to have met whatever standard is in place. Then at the end of the semester, each student determines what their grade in the course will be --- making an argument for their choice based on evidence drawn from their work.

So ungrading removes marks from the picture, ostensibly in order to focus student attention on the work itself and engagement with the feedback loop. The point is to remove distractors (and marks are absolutely distractors) and build metacognition and self-evaluation skills, while at the same time giving students ways to grow in their learning over time.

I decided to revamp my course to be ungraded because most of the work consists of written mathematical proofs of theorems. Like any kind of writing, proofs benefit from iteration and feedback. In the past I'd set up the course to use specifications grading which had those feedback loop systems in place and this worked very well --- except for the marks. Students' proofs were graded on the EMRF (later changed to "EMRN") rubric, which I felt was pretty simple and inobtrusive. But even with just four marks available, the specs grading requirements (for example, you needed at least 3 "E" grades on proofs to earn a B in the class) diverted student attention to the number of E's they'd earned, and away from thinking about what sort of work earns an "E" in the first place and what aspects of their current drafts were attaining this or missing the mark.

In other words I wanted students to focus more on the work than on the mark. In the end I determined that the only way to make this happen was to throw out the marks.

How it worked

Each week students got two homework problems, which were proof-based problems to work out. Students also did Daily Prep assignments in which they worked out some details of a new concept and then put together a preliminary solution to other problems and were tasked with volunteering to present their work on these in class. I had a system for selecting volunteers to actually present the work based on how many times they'd done it before and how recently.

None of this work received a grade.

Homework problems were turned in each week and given extensive feedback, including notes about whether the work met standards for proofs given in a list of homework objectives. In the LMS gradebook, I just put a "1" if the homework was submitted and "0" otherwise. Students could revise and resubmit one problem per week, including problems that belonged to homework sets that they didn't turn in earlier.

The presentations weren't graded either. They didn't need to be. Students were the audience for the presentations, and if there were questions, they took care of those. Sometimes presentations had errors in them; that made for good discussion and class activities. (Although I told them that correctness was not a criterion for being selected to present, if their work had major errors in it, I'd give them feedback on that and not make them present.)

All semester long students have been doing this work, alternating between homework and Daily Prep. Some problems from our list ended up being class activities, and students could also opt to write up a solution to one of them and submit to a "Class Journal", as a kind of optional homework. Again, no grades on anything, just feedback. Here is what the syllabus says about how to earn a course grade:

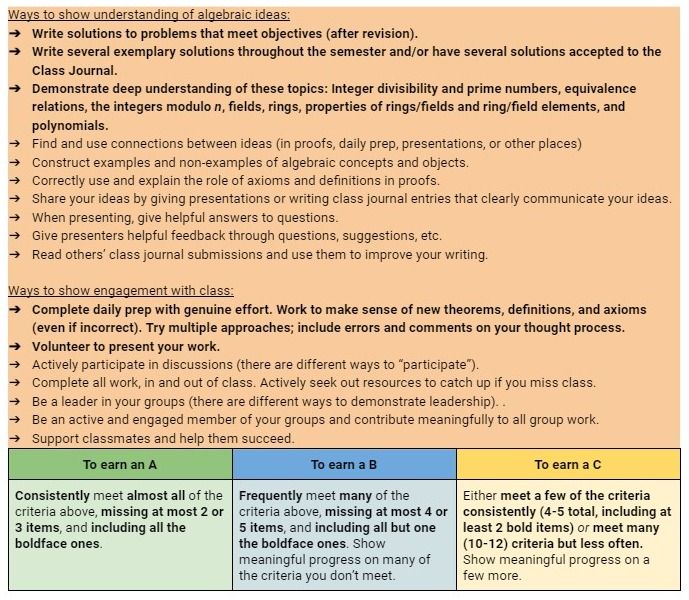
In the end, students will be assembling a Portfolio of their work, drawn from a collection they choose, and making a request for a course grade and presenting their work as evidence that they've earned the grade.

What's been good

There are a lot of things that I've liked about the ungrading approach in this class:

• I know my students better than I ever have. I'll be honest, in the past, I've made it to week 11 and still didn't know the names of half my students. But I've learned that ungrading only works if you have lots of communication with students. So I've held one-on-one meetings with each student once (back in week 5) and several students twice (last week) to make sure they're calibrated and to get their thoughts on their work. There's so much feedback going on that I feel like I've gotten very familiar not only with names and faces but also strengths and weaknesses. You can't always have this level of contact in a class but I feel like this is the level to which I aspire from now on.
• There's much less talk about "what the teacher wants". One of the most disappointing things about classes like this in the past is that students always framed their work in terms of "what Prof. Talbert is looking for". A student would turn in a proof by contradiction with an incorrectly-stated assumption; I'd give feedback to that effect and the work would be revised, but the student would want to know "Is this what you were wanting?" I wanted to shout "It's not about what I want!" In ungrading, since marks are absent and the focus is very clearly on the work itself, I have literally not heard this conversation at all.
• Students are cool with this. Like I said, I've had a lot of contact with students, and they've had plenty of chances to complain about ungrading if they wanted, but for the most part it's just not been a big deal. Nobody has brought the grading system up at all; I have not had to seek any "buy-in". To the extent we've discussed it, students have wanted some clarification on the portfolio (which I addressed in this document) but to them, I think it just makes sense.

What I've noticed/what's been less good

I wouldn't say that I've encountered a lot of "issues" with ungrading. But there have been a few things that make me stay skeptical about it, even as I've used it.

The main one is that ungrading seems to work only as well as students' abilities to self-evaluate. The building of skills in self-reflection and metacognition is one of the goals of ungrading, but those skills are also among its ingredients. If a student lacks those skills coming into an ungraded class, then you can give all the helpful feedback you want, but that student will struggle more to make sense of it than will another whose skills are better developed. While I have really enjoyed my students, it is an objective fact that their background knowledge in mathematics in general and proof in particular is very widely varied. This isn't a complaint; it's just a persistent fact about working in higher ed, and my job is to deal with it. But in ungrading, those variations seem to be amplified because the entire assessment scheme is based on self-evaluation. So I'm not sure that ungrading is serving the lower end of this spectrum --- the students who work hard but don't have the best grasp on the basic tools of the discipline --- as well as it is serving the upper end.

And this makes me wonder if ungrading actually contributes to some of the equity gaps we struggle with in higher education, particularly in STEM, rather than alleviating them. There is evidence that alternative grading systems in general can help with those gaps. But by removing marks from the picture, I wonder if it takes away the guideposts that learners from less-privileged backgrounds might need as they navigate college courses --- like if someone took away all the signs in the airport in a foreign country and you dropped a non-native language speaker into it. Sure, there's a possibility that a person would focus more on the signs than on the journey they're taking; but those signs can definitely be helpful, as well.

Also, some people have suggested that ungrading shifts more work onto the backs of students by making them responsible not only for understanding the material itself but in determining whether that understanding is real and where it needs to be improved. I don't think I fully agree with this, since students are definitely not solely responsible for self-evaluation, and anyway I feel like self-evaluation is one of the learning outcomes of the course. But I also think there's some truth to this: It's definitely more work for students, because they are responsible for self-evaluation. The benefits outweigh the costs in my view, but you can't deny the cost to students is nonzero, and it's something we need to think about.

My verdict (for now)

It was a good idea to use ungrading in this class, because it seems like a compelling fit to the content, the students, and the level at which it's offered. But I'm not sure I would do it again.

Among the issues I noted above, at this point I'm not sure if ungrading is significantly more beneficial than, or even different from, plain old specifications grading. My students are generally pretty good at taking feedback and doing something useful with it; but many are still building the metacognitive skills needed to know the extent to which their work meets expectations in the first place and therefore anticipate that feedback. Semantic errors are a huge contributor here, for example if a proof features an equation that has a matrix on one side and an integer on the other; or an attempt to find the greatest common divisor of two equivalence classes. These and others are real errors, but many students are still building the mathematical sophistication needed to notice them.

So eventually I end up telling students explicitly whether their work meets expectations or is exemplary. For example I might write:

Your work on Problem 1 definitely meets the homework objectives! It shows solid understanding of the main concepts and is correctly reasoned and explained.

Or:

Your work on Problem 1 is exemplary. It shows a strong grasp of the concepts, and the communication is excellent.

But if I need to give students explicit language about "meeting homework objectives" and "exemplary", why not just use specifications grading with marks for those things? How is ungrading any different than specs grading with a three-level rubric (Exemplary/Meets Objectives/Needs Revision)? Seems to me that if students really need that explicit "signage" then we should give it to them.

I suppose the question is whether they need it. I've seen this handled by other professors by giving feedback until it gets to the point where the feedback is "I have no more feedback to offer on this, congratulations". I haven't been doing that, and perhaps that's a mistake. But I also feel like my way saves students time and effort because it gives explicit guidance where otherwise they would be operating using self-evaluation skills that are still in progress.

But how will students get to the point where they can effectively self-evaluate if you keep telling them explicitly whether their work is good enough? you may ask. It's a fair question. Perhaps it takes a key element of work in the class off their plates and that's a mistake. But I see it as work off their plates which seems like a good thing.  

This course isn't on my schedule for the next year, so I have the space to think about it. I think it's possible to have a hybrid setup in a lower-level course (like I'm teaching this summer) where the work that addresses the lower reaches of Bloom's Taxonomy is graded using specifications with marks, while the upper levels of Bloom are ungraded (or graded using a Pass/No Pass rubric). I don't feel like ungrading is the logical conclusion of grading systems --- as in, "If you really cared about students, you wouldn't use grades at all", as if ungrading was some morally perfected form of specifications grading. I think ungrading is a tool, an approach to assessment that has its own set of pros and cons, and works well in some contexts and less well in others.

The important thing, instead, is to keep student growth at the center and give them a grading system that's optimized for that growth --- whether or not it includes marks.