Grading for growth in an engineering math class: Part 1

This post first appeared at Grading For Growth earlier this month. There is a second part as well which I'll repost here later, or you can just click and read it now. I've added some new thoughts to the end of this post just for rtalbert.org readers!

With summer officially underway, I'm going to be writing for the next two weeks about the grading system I had in place for the semester that just ended, in my Linear Algebra and Differential Equations classes. David wrote a couple of posts on his experiences (part 1, part 2) and mine will be along the same lines.

The first installation today is about the "theory" of the class -- all the background information about the class and my philosophy of teaching it that led to the grading process that I used. Next week, I'll focus on the "practice" -- how it was received by students, what worked and did not work in real-life practice, and what I'll do again and do differently next time.

For reference, here are some links for the class:

• The class GitHub respository (which contains everything) — it’s all Creative Commons licensed so help yourself to whatever you like, just give attribution to me (Robert) if you use something.
• The syllabus
• Standards for Student Work document

What was the class?

The class that I taught was MTH 302: Linear Algebra and Differential Equations. This is a four-credit course primarily intended for students in engineering that combines topics from these two gigantic areas of mathematics. I taught two sections, each two hours long, back-to-back on Tuesdays and Thursdays. Enrollment hovered around 30 students in each section, and all the students were second- or third-year engineering majors (with the exception of one lone Accounting major who was working on a math minor).

You'll find versions of this course at many universities that offer engineering degrees, and it's clear that many profs who teach it don't quite know what to make of it. Linear Algebra and Differential Equations, as separate subjects, are significant enough to merit two required courses each, but in MTH 302 we put them both into a single class. There are two ways to handle this kind of compression. One is to build the course around a small, reasonable core of content and learning outcomes that necessarily leaves out some interesting math, and then set up structures to help students learn those things deeply. The other way, which is seemingly far more common, is to leave nothing out, and just Cover All The Things at an enhanced speed and diminished depth, trusting that the "good students" will somehow keep up.

The Cover All The Things approach makes the course tend toward procedural rather than conceptual knowledge (because conceptual knowledge is slow cooking), so the course ends up as a hyper-accelerated flythrough of a cookbook, with a lot of the best recipes missing. The experience for students and instructors alike becomes impoverished, uninspiring, and aimless.

Those three adjectives also describe many of my students' past experiences with math courses, including MTH 302's prerequisites of Calculus 1, 2, and 3. Every student in MTH 302 has completed these; a good portion of my students "completed" them as though escaping through a fire. Don't get me wrong: MTH 302 students are high-achieving and highly capable. But many were simply Calculus survivors, with a survivor mentality about Calculus and other forms of math.

And not to get ahead of myself, but when you've had experiences akin to Covering All the Things in a traditionally-graded system, the survivor mentality goes into overdrive. If you have to learn how to compute things correctly by hand, assessed by one-and-done tests with no feedback loops, every day in class is about survival.

My approach to the class

I'd taught Linear Algebra before, and Differential Equations before, but never this weird mashup. I certainly wanted to avoid the negative experiences with the class I'd seen elsewhere. My first order of business, then, was to make the class less weird, by answering the question: What is this class about? I don't mean, What topics does it cover or What does the catalog say. Instead I mean the same thing as when we ask someone what a book or a movie is about.

As I looked at the individual "halves" of the course -- linear algebra, and differential equations -- and how those two subjects interact, I decided that MTH 302 is about modeling systems that undergo change, and seeing what we can learn about those systems from the models. This felt right: Both topics grow out of the need to model real-life systems like ecosystems and spring-mass systems, that change and evolve over time and whose behavior we want to predict.

When you decide what a class is about, you are also deciding what it is not about. In my case, for example:

• While there are mathematical computations to learn in MTH 302, the class is not about mathematical computation: It's about using the results of computation to say something insightful about a model of a system.
• While some problems in MTH 302 may have right answers, the class is not about right answers: It's about understanding and communicating what the answers tell you, and evaluating the assumptions used in the model that led to those answers.

I was beginning to get a glimpse of the learning objectives for this course, and what students might do to provide evidence of learning. Pretty soon the grading approach would be on the horizon.

By the way, if this process sounds familiar, it’s because I’m following the workflow that I wrote about last summer in the mini-series “Planning for Grading for Growth”, which will also be appearing in David’s and my forthcoming book as a workbook chapter. You can read that series here, which is the final article in the series but has links to all the preceding articles.

On a more immediately practical level, I had factors to incorporate into the design of the class at this point. First, as I said, I'd never taught this particular class before, so I wasn't too interested in any radically different approach from what I had used in the past elsewhere. Second, and related, this was a service course for the Engineering school, and I didn't (and still don't) have a great sense of their tolerance level for "far out" pedagogical practices. Third, the students in the course, being engineering majors, were maxed out with a demanding set of courses in their discipline, and I was very hesitant to create a wild new course structure that demanded more cognitive load than necessary.

In particular, I decided at the outset that I would not use ungrading in the course. Since that term is so ambiguous, what I mean is that I would not do what David did in his geometry course or which I did in my Winter 2022 abstract algebra course, where student work got no grades but just feedback, and we collaboratively decided on course grades at the end. I don't think it would have been absolutely wrong to do this with MTH 302; but relative to my newness with this course and what I understood about the constraints on students, it didn't seem like the right call. However: Come back next week for more thoughts on this.

How did the class work?

I mentioned earlier that each class session was 2 hours long. Students were doing things before, during, and after class:

• Before class: Students would complete a Class Prep assignment in which they did some initial reconnaissance work on the new upcoming topics, usually by watching some video or reading text and then completing some basic exercises, and asking questions along with those exercises. Class Preps were due the night before class, so I could scan them in the morning to look for trouble spots and frequently asked questions.
• During class: We'd start each meeting with 15 or so minutes of Q&A time over the Class Prep, clearing up questions and the like. Then there would usually be a short demo from me to set up an activity. Then, students would work in groups at their tables on activities to provide practice with the new topics. Here is a folder at the GitHub repository with many of the activities. As you can see, some of the activities are starred, indicating that students will work on those in groups during class but write up their own solutions separately for later turn-in. The writeups of select group activity problems were called Application/Analysis assignments. We'd typically run the activities for 30 minutes or so, then 10 minutes to debrief and field questions, at which point we'd be at the one-hour mark. We'd take a 5 minute break, then come back and do the same thing for another hour, then end with questions and announcements and go home.
• After class: Outside of class, students were prepping for the next class, finishing up their Application/Analysis writeups that they began in class, and completing Miniprojects which I'll say more about in a minute.

What you'd see if you walked into a typical class would be 6-8 groups of 3-4 students doing heads-down work on a problem that guides them toward understanding of some important learning objective of the course. Sometimes students went to the board to work; other times just working quietly, but very often not quietly, with their friends. My role was to be everywhere all at once, going from group to group to answer questions, prod people along with questions, and check to make sure everyone was OK and progressing.

How did students provide evidence of learning?

I've always felt that there were three more-or-less independent axes along which success in a course should be determined: mastery of basic skills, mastery of applying those basic skills to new situations, and what you might call "engagement" or "being in the course". An "A" student is one who can demonstrate consistent excellence along all three axes. A "C" student is one who is "just good enough" on the first two axes and makes a reasonable effort on the third. That 3D axis model seemed to fit particularly well in MTH 302, where there were a lot of basic skills that are important to master, as well as a large helping of applications to master as well.

Students gave evidence of their progress along these axes via five major forms of assessment in the class.

• Class Preps: I mentioned these above. Here's a typical example. These are mainly in place so students will get the gist of the basics of new ideas, so that we can get a running start in class. They are graded on the basis of completeness and effort: Put in a good-faith attempt at a right answer for each non-optional item, and you receive a mark of "Success" which means full credit. Otherwise it's a mark of "Incomplete".
• Skill quizzes: Although the class isn't about computation, it was still valuable to isolate a few Foundational Skills for students to learn how to do by hand. I ended up settling on eleven Foundational Skills which you can find in this appendix of the syllabus. The vast majority of times we needed to use one of these skills, we'd do it with a computer; but they are central enough that I wanted students to demonstrate they could do them in simple situations by hand with no significant mistakes. Every week on Thursday, we set aside the last 30 minutes of the class for quizzes over these skills. Here's a typical quiz showing some typical problems for some of the skills. Each skill appeared on three consecutive quizzes, then disappeared until one big "last chance" quiz at the end. Students had to complete a problem for a skill once, meeting all the "success criteria" shown on the quiz, at which point they had demonstrated sufficient skill.
• Application/Analysis: Also mentioned above. These were turned in weekly and consisted of selected parts of in-class group work. So students worked on them in groups along with other problems, then wrote individual solutions up of the selections.
• Practice problems: We didn't focus much on very basic computation during class. That was the subject of practice problems, which were weekly problem sets on our online homework system.
• Miniprojects: Finally, the heart of the course were eight Miniprojects covering various applications and extensions of linear algebra and differential equations concepts learned in class. Here's one; here's another. The focus of miniprojects is on applying basic concepts to new problems and on communicating results and processes in written form in a coherent and professional way. These were done outside of class, and had a flexible deadline structure.

Practice problem sets and Foundational Skills via the quizzes assessed along the “basic skills” axis; Miniprojects assessed along the “apply basic skills to new things” axis; and I considered Class Preps to be more “engagement” than anything else. Application/Analysis was a late addition to the syllabus, and I almost didn’t add it at all in order to keep things as simple as possible. But without those, it felt like something was missing, namely an assessment in the space in between the lower and upper thirds of Bloom’s Taxonomy. That middle third of Bloom is labelled “Application” and “Analysis”, hence the name of the assessment. I would have second thoughts on several occasions about including this; see next week’s article for more.

How individual work was graded

With the context, philosophy, and assessments all laid out, we can now talk about the grading system. All the criteria for grading different forms of work is spelled out in this document called Standards for Student Work in MTH 302. To summarize:

• Class Preps were graded either "Success" or "Incomplete" based on completeness and effort. There were no reattempts allowed since Class Preps are time-sensitive and only viable assessments if done before class.
• Practice problems were auto-graded by the online homework system, with each problem receiving 1 point for a correct answer and 0 for incorrect with partial credit sometimes available.
• Problems on Skill Quizzes were graded either "Success" or "Retry" based on whether the student's work met the "success criteria" listed on the problem. Each skill appeared on three consecutive quizzes, so if you got a "Retry" you'd try again on a new version of that problem in the following week.
• Application/Analysis submissions were graded "Success", "Retry", or "Incomplete" based on completeness, effort, and "overall correctness". (Some minor mistakes were allowed but anything serious required redoing.) These were turned in on our LMS; work marked "Retry" or "Incomplete" would get lots of written feedback on the submission, and students were allowed to submit a single revision.
• Miniprojects were also graded "Success", "Retry", or "Incomplete" based on completeness, effort, correctness, and organization. Specific requirements for "Success" were given on the Miniproject forms. These usually involved a combination of math, English, and Python code and were written up in Jupyter notebooks, and the notebooks submitted in the LMS. They'd then get written feedback, and revisions could be done if needed.

On the last two, the difference between "Retry" and "Incomplete" is mainly terminology. Either mark could be removed through a reattempt or revision. An "Incomplete" indicates that there was something serious missing from the submission that made it impossible to grade the work: A missing problem, a tangle of significant semantic or math errors, code that won't compile, a Google Doc with the permissions incorrectly set, and so on. If a student's work was incomplete, I'd stop grading immediately, assign the mark, and tell them I'll look closely at their work once they submit something that's complete.

How course grades were assigned

I said we shouldn't try to label the form of grading I was doing here, but if you must add a label, this is pretty much specifications grading, such as I've used in most of my courses since 2017. It features 2- or 3-level grade rubrics on each item, with those items being graded holistically according to specifications that are clearly spelled out.

My course grade assignment method was specs grading-like as well, with course grades being determined by counting up accomplishments. The syllabus uses this table:

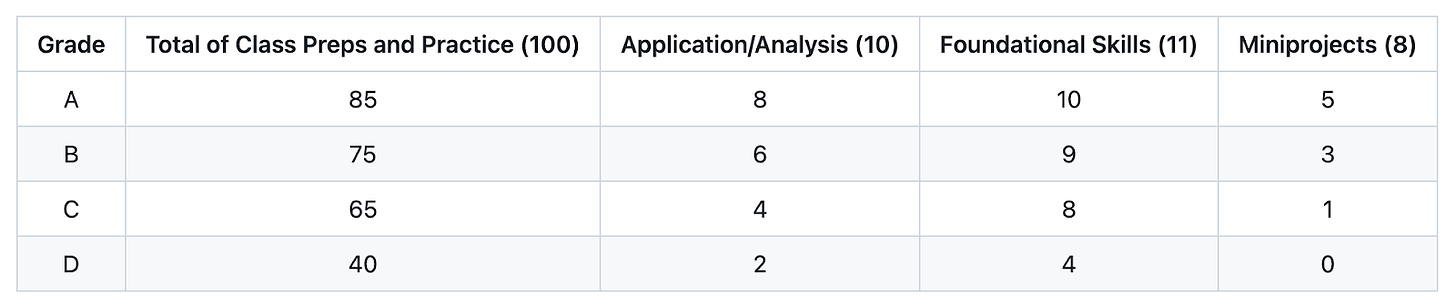
A student's course grade is the highest row for which all the requirements of the row are satisfied. That establishes the "base grade" of A, B, C, D, or F. There are some rules in the syllabus guiding the assignment of plus and minus grades as well that involve a final exam. The only effect the final exam had on the course grade was to potentially add plus or minus modifiers to the base grade.

I turned this syllabus table into a checklist for students to use to track their grades:

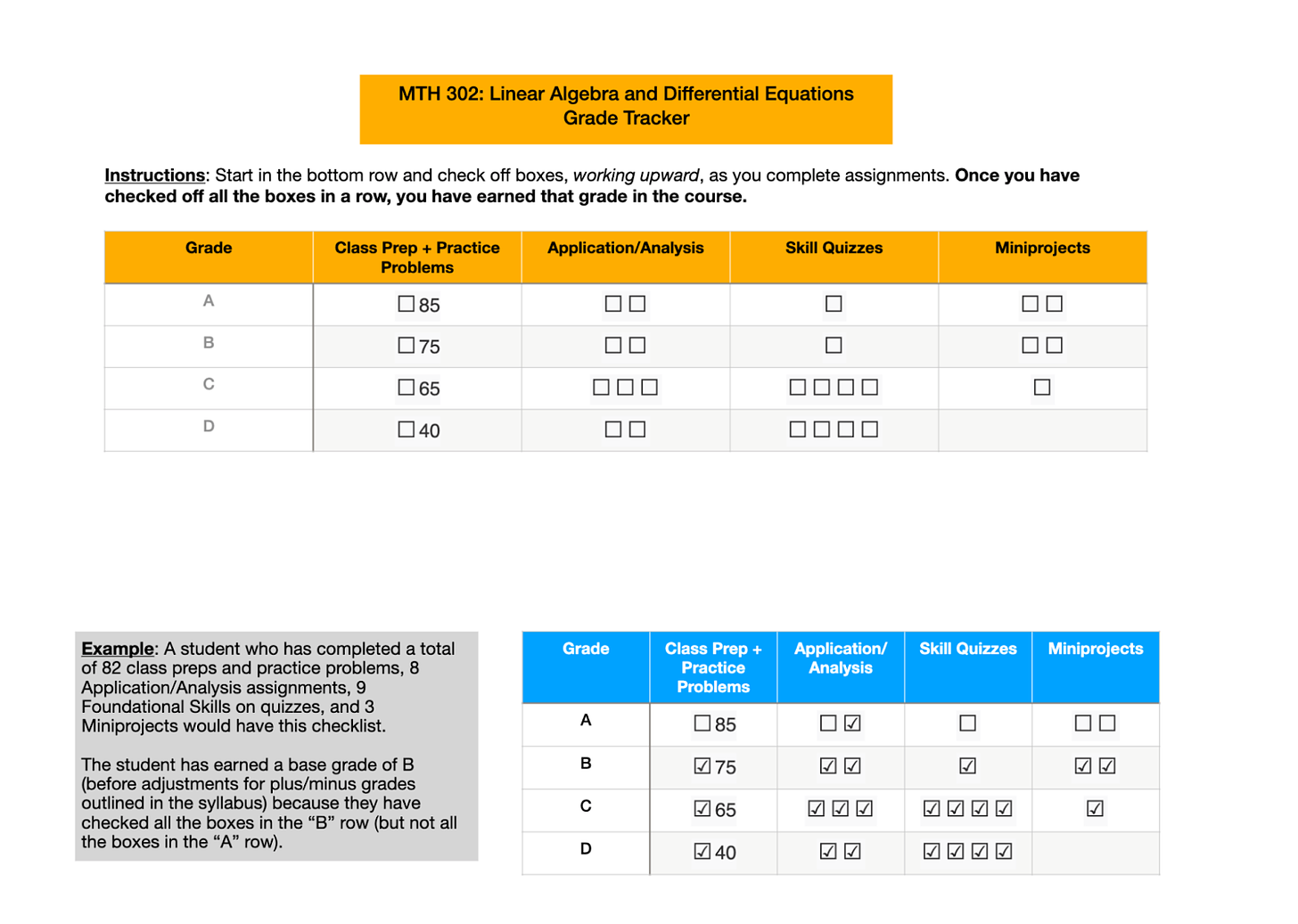
They just had to print it out or keep it on their tablets, and check boxes as they accomplished things.

What’s next

That's more than enough detail for now, although if you have specific questions you can probably find the answers in the syllabus; ask a question in the comments if not.

Next week, I'll continue this story by writing about what happened when this system made contact with students. Would they like it? Would they be confused by it? Would it make them question their existence and see beyond the universe itself? You'll need to tune in next time to find out.

Updated thoughts

• There's a question running in the background of this article that I think is interesting: How far do you push innovation in a course that is a service course for another department? Here, MTH 302 serves our Engineering school. I have a good relationship with the students and faculty in this school, but as I mentioned, to this day I don't have a great read on how tolerant they are of teaching innovations. My sense is that most of the faculty are quite traditional, a sense that is supported by what my students describe from their other classes. So when I approached this class, I deliberately throttled back on the innovation – for example I still used a final exam and we still had homework – because I wasn't sure how some of my ideas would land. I'm not sure how you go about working more innovation into a course like this, besides building things up slowly over the course of several semesters and earn the trust of the other department.
• There is an interesting comment thread at the original post about my choices for distinguishing between a "D" and an "F" in the course. I could go into this more, but it's pretty basic for me: I don't really think too hard about "D" grades. It's the "C" grade that matters to me: That grade should mean "minimum baseline competence that makes me feel comfortable the student can succeed at the next level" (whatever "next level" means). So if that's the case, what is a "D"? For me, means that the student didn't totally abandon the class, and success at the next level is possible. So I won't try to prevent a student with a D from going on to the next course, but I would leave that choice up to the student and their advisor. (Although it's moot in many cases, for example our engineering school requires retaking the course if the grade is C- or less.)