Three questions to ask about designing active learning tasks

I'm working with a group of faculty at another university right now who have an NSF grant to convert three of their mathematics courses over to primarily active learning pedagogy. Yesterday I did a workshop (over Zoom, of course) to help them think about how they might carry out this conversion. The first part of the workshop was about the theoretical background of how people learn, and research about active learning; the second part focused on specific examples of active learning exercises for students in Calculus.

Making out those examples, I realized – somewhat horrified – that after all these years doing active learning in my classes, I'd been failing to ask three important questions about active learning. At least I have not asked all three questions consistently, and had I done so, my students might have had better learning experiences.

It started with this example from an image search on "calculus lecture notes".

Having grabbed this image, I thought to myself: How can we turn this from an example in a lecture, into a task for students that can get them actively engaged? But that's when it hit me that that's not how this works, and unless there are three things cleared up first, we're not ready to do active learning with this task.

What is the learning objective?

I've written a lot about learning objectives lately, because I believe that good teaching and learning starts and ends with having clear, observable learning objectives. When you have them, and all the other components of the course are aligned with those objectives, good things happen. Without them, it becomes difficult to know if our teaching is having the desired effect of helping our students learn – because we haven't clearly stated what students are supposed to be learning.

If I just took the above problem and turned it into an active learning task, I might run into trouble because I haven't asked, What is the learning objective to which this problem is connected? It's fairly easy to reverse-engineer the learning objective, which might be phrased, Find the critical points of a function. What I should do is state it explicitly at the beginning of the task: This task relates to Learning Objective 3.4 or however I have labeled the learning objective in my syllabus.

Explicitly stating the learning objective in the task itself helps the students understand why they are doing the task. But it also helps me, because when I look at this problem alongside the learning objective, a couple of questions arise.

First, does the task actually connect to the learning objective? A learning activity connected to a learning objective is supposed to provide students practice with that learning objective. Does this one do that? I think so – the task is all about finding critical points of a particular function, so the connection isn't tenuous or tangential.

Second, does the task introduce extraneous cognitive load? If a student fails at this task, does it mean they are failing at the learning objective, or is there something else that is causing trouble? Here's where this task has some issues. If I gave this task to a student, and they get stuck, it could be because they are unclear on what a critical point is and how to find one. But it's also possible they could just be struggling with trigonometry. A student might know they need to differentiate $f(x) = 2 \cos (x) + \sin^2 (x)$ and then find the zeroes; and they might be OK with the derivative; but finding a general form of the zeroes of $f'(x)$ is a nontrivial task that is not directly related to the learning objective. So we should ask: Is there a simpler way to address the learning objective?

That doesn't mean that students should never work on complex tasks. It just means that we need to be careful about the construct validity of our active learning tasks, so that we don't end up getting a lot of false negatives because students struggle with a sub-task that is not related to the learning objective that the task addresses. And we can't do that unless we identify the learning objective.

Is it pitched at the right level?

Let's say the above task is repackaged as follows:

(This task addresses Learning Objective 3.4.) Find all the critical points of the function $f(x) = 2 \cos (x) + \sin^2(x)$. Work by yourself for 3 minutes, then complete the work with a neighbor for 2 more minutes.

And let's ignore the concern above about extraneous load. There's another question to consider, which is, Is this task at an appropriate level of Bloom's Taxonomy?

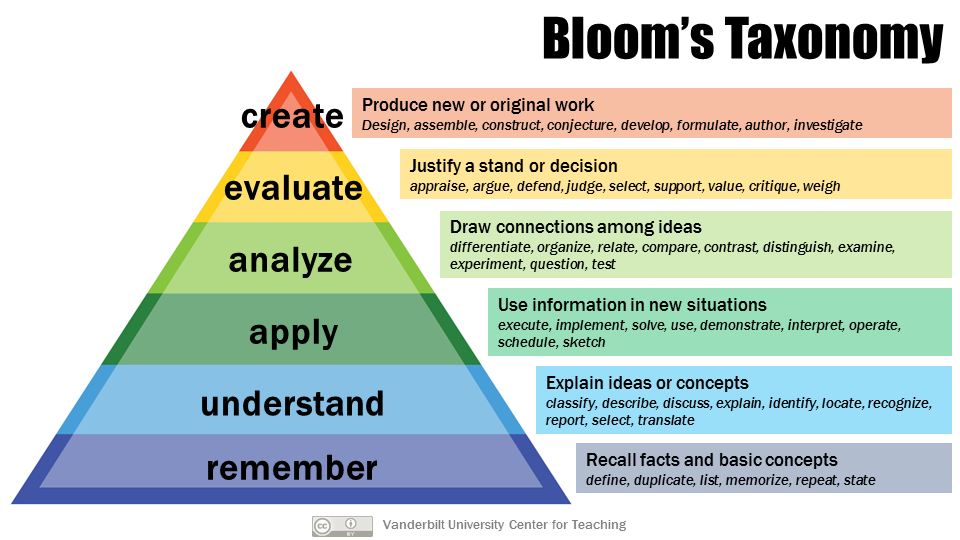
The above task is probably on the Apply level. Is that where I want it? Obviously it depends on where the task is situated relative to the lesson and the other tasks and objectives within it. The task as stated might be at the right level; or it might be too complex, or not complex enough. It depends. And so we have to ask.

If this were students' first attempt at working with critical points, then even ignoring the trigonometry issues, this task is way too complicated. We should probably remix it so it's in the "Understand" or "Remember" levels. Here's a possibility:

Consider the graph of $f(x) = 2 \cos(x) + \sin^2(x)$ below on the interval $-\pi/2 \leq x \leq 5\pi/2$. How many critical points does the function have on this interval? (a) 0; (b) 1; (c) 2; (d) 3; (e) 5; (f) None of these

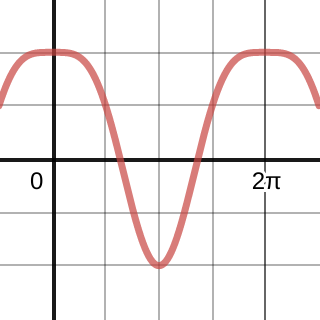
Students are still addressing the objective Find the critical points of a function but instead of calculating them (including a lot of pesky trig) they are "identifying" or "locating" them, both Understand tasks and probably more suitable if students are just getting started.

Or maybe we're close to the end of the module and we want students to do more than just crank out calculations. We could have them do something like this:

Fred is trying to find the critical points of $f(x) = 2 \cos(x) + \sin^2(x)$ on the interval $-\pi/2 \leq x \leq 5\pi/2$. He takes the derivative to get $f'(x) =-2\sin(x) + 2 \sin(x) \cos(x)$, then factors to get $f'(x) =2 \sin(x) (\cos(x)-1)$.  He concludes that either $\sin(x) = 0$ or $\cos(x) = 1$, therefore $x = \pi$ and  $x=2\pi$ are critical points because $\sin(x) = 0$ there. He also includes $x = 0$ as a critical point because $x=0$ must always be a critical point of a function. What, if anything, could be corrected or improved about Fred's reasoning?

This is an Evaluate task, fairly high on the pyramid and (in my experience) a great exercise for students who have been through the mechanics of the learning objective and now need to think more critically. (In case you're wondering, every time I teach calculus I get a horde of students who believe that $x=0$ has to always be a critical number of every function. Where does this come from?)

There's one last question that wasn't something I considered until nowadays.

How does it work in an online setting?

With the sudden advent of online teaching basically everywhere and for the foreseeable future, we have think about how active learning tasks work in an online setting. The good news is that it's quite possible to deploy active learning tasks in an online setting, and in fact students want this. (I know this indirectly by the amount of justified complaining I've heard about profs whose online courses are nothing but lectures.)

The original example here could be done online by giving it to students and telling them to work out the solution and post it to the course discussion board. That's... OK. But it seems boring and non-interactive. Improvements might include:

• Pairing students off and having them work through it in a direct message or private chat area first, then posting the results for discussion.
• Giving students a spot on a Google Jamboard and having them work it out (click the link to see an example).
• Having students write their solution up on a whiteboard or piece of paper, make a video of themselves doing so, and posting it to FlipGrid for discussion

Notice these all leverage the unique affordances of an online course, especially the ease of inclusion of multimedia.

The variations on this task also work well online. The multiple-choice identification version of the task fits right in with the quiz system of an LMS, a multiple choice item on a Google Form, or an online polling tool. The evaluation version of this task would be a good discussion board or FlipGrid prompt.

We can't just take our lecture notes, give the examples out to students to do themselves, and call it a day. We have to make sure active learning tasks clearly instantiate a learning objective, that they are pitched at the right level, and that they are online-ready. I think I understand this myself now, and I think it will make my active learning designs a lot more student-friendly and effective.